Série de Fourier de funções periódicas de período 2π.
A série de Fourier permite estudar funções periódicas decompondo-as em componentes. correntes alternadas e tensões, deslocamentos, velocidade e aceleração de mecanismos de manivela e ondas acústicas são típicos exemplos práticos aplicação de funções periódicas em cálculos de engenharia.
A expansão da série de Fourier é baseada na suposição de que todos valor prático funções no intervalo -π ≤x≤ π podem ser expressas como séries trigonométricas convergentes (uma série é considerada convergente se uma sequência de somas parciais composta por seus termos converge):
Notação padrão (=usual) através da soma de senx e cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 senx+b 2 sen2x+b 3 sen3x+...,
onde a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. são constantes reais, ou seja,
Onde, para o intervalo de -π a π, os coeficientes da série de Fourier são calculados pelas fórmulas:
Os coeficientes a o , a n e b n são chamados Coeficientes de Fourier, e se eles puderem ser encontrados, então a série (1) é chamada perto de Fourier, correspondente à função f(x). Para a série (1), o termo (a 1 cosx+b 1 senx) é chamado de primeiro ou gaita principal,
Outra maneira de escrever uma série é usar a relação acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Onde a o é uma constante, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 são as amplitudes dos vários componentes e é igual a a n \ u003d arctg a n /b n.
Para a série (1), o termo (a 1 cosx + b 1 senx) ou c 1 sen (x + α 1) é chamado de primeiro ou gaita principal,(a 2 cos2x+b 2 sin2x) ou c 2 sin(2x+α 2) é chamado segundo harmônico e assim por diante.
Para representar com precisão um sinal complexo, geralmente é necessário um número infinito de termos. Entretanto, em muitos problemas práticos é suficiente considerar apenas os primeiros termos.
Série de Fourier de funções não periódicas de período 2π.
Decomposição de funções não periódicas.
Se a função f(x) for não periódica, então ela não pode ser expandida em uma série de Fourier para todos os valores de x. No entanto, é possível definir uma série de Fourier representando uma função em qualquer faixa de largura 2π.
Dada uma função não periódica, pode-se compor uma nova função escolhendo valores de f(x) dentro de um determinado intervalo e repetindo-os fora desse intervalo em intervalos de 2π. Como a nova função é periódica com período de 2π, ela pode ser expandida em uma série de Fourier para todos os valores de x. Por exemplo, a função f(x)=x não é periódica. No entanto, se for necessário expandi-lo em uma série de Fourier no intervalo de 0 a 2π, então uma função periódica com período de 2π é construída fora desse intervalo (conforme mostrado na figura abaixo).
Para funções não periódicas como f(x)=x, a soma da série de Fourier é igual ao valor de f(x) em todos os pontos do intervalo dado, mas não é igual a f(x) para pontos fora da faixa. Para encontrar a série de Fourier de uma função não periódica no intervalo 2π, usa-se a mesma fórmula dos coeficientes de Fourier.
Funções pares e ímpares.
Eles dizem que a função y=f(x) até se f(-x)=f(x) para todos os valores de x. Gráficos de funções pares são sempre simétricos em relação ao eixo y (ou seja, são espelhados). Dois exemplos de funções pares: y=x 2 e y=cosx.
Eles dizem que a função y=f(x) ímpar, se f(-x)=-f(x) para todos os valores de x. Gráficos de funções ímpares são sempre simétricos em relação à origem.
Muitas funções não são nem pares nem ímpares.
Expansão em série de Fourier em cossenos.
A série de Fourier de uma função periódica par f(x) com período 2π contém apenas termos de cosseno (ou seja, não contém termos de seno) e pode incluir um termo constante. Consequentemente,
onde são os coeficientes da série de Fourier,
A série de Fourier de uma função periódica ímpar f(x) com período 2π contém apenas termos com senos (ou seja, não contém termos com cossenos).
Consequentemente,
onde são os coeficientes da série de Fourier,
Série de Fourier em um semiciclo.
Se uma função é definida para um intervalo, digamos 0 a π, e não apenas 0 a 2π, ela pode ser expandida em uma série apenas em termos de senos ou apenas em termos de cossenos. A série de Fourier resultante é chamada perto de Fourier em meio ciclo.
Se você deseja obter uma decomposição Fourier em um meio ciclo em cossenos funções f(x) no intervalo de 0 a π, então é necessário compor uma função periódica par. Na fig. abaixo está a função f(x)=x construída no intervalo de x=0 a x=π. Como a função par é simétrica em relação ao eixo f(x), desenhamos a linha AB, conforme mostrado na Fig. abaixo de. Se assumirmos que fora do intervalo considerado, a forma triangular resultante é periódica com um período de 2π, então o gráfico final tem a forma, display. na fig. abaixo de. Como é necessário obter a expansão de Fourier em cossenos, como antes, calculamos os coeficientes de Fourier a o e an
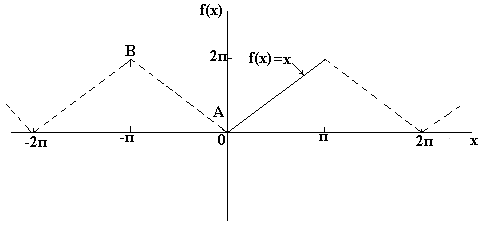
Se você precisa obter Expansão de Fourier de meio ciclo senoidal função f(x) no intervalo de 0 a π, então é necessário compor uma função periódica ímpar. Na fig. abaixo está a função f(x)=x construída no intervalo de x=0 a x=π. Como a função ímpar é simétrica em relação à origem, construímos a linha CD, conforme mostrado na Fig. Se assumirmos que fora do intervalo considerado, o sinal dente de serra recebido é periódico com período de 2π, então o gráfico final tem a forma mostrada na Fig. Como é necessário obter a expansão de Fourier em um meio ciclo em termos de senos, como antes, calculamos o coeficiente de Fourier. b
Série de Fourier para um intervalo arbitrário.
Expansão de uma função periódica com período L.
A função periódica f(x) se repete à medida que x aumenta em L, ou seja, f(x+L)=f(x). A transição das funções de período 2π consideradas anteriormente para funções de período L é bastante simples, pois pode ser feita por meio de uma mudança de variável.
Para encontrar a série de Fourier da função f(x) no intervalo -L/2≤x≤L/2, introduzimos uma nova variável u de modo que a função f(x) tenha um período de 2π em relação a u. Se u=2πx/L, então x=-L/2 para u=-π ex=L/2 para u=π. Seja também f(x)=f(Lu/2π)=F(u). A série de Fourier F(u) tem a forma
(Os limites de integração podem ser substituídos por qualquer intervalo de comprimento L, por exemplo, de 0 a L)
Série de Fourier em semiciclo para funções dadas no intervalo L≠2π.
Para a substituição u=πx/L, o intervalo de x=0 a x=L corresponde ao intervalo de u=0 a u=π. Portanto, a função pode ser expandida em uma série apenas em termos de cossenos ou apenas em termos de senos, ou seja, dentro Série de Fourier em um meio ciclo.
A expansão em cossenos no intervalo de 0 a L tem a forma
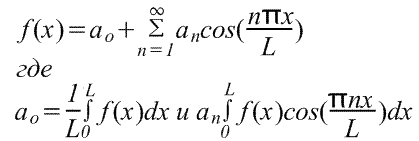
Que já estão bastante fartos. E sinto que chegou o momento de extrair novas conservas das reservas estratégicas da teoria. É possível expandir a função em uma série de alguma outra maneira? Por exemplo, para expressar um segmento de reta em termos de senos e cossenos? Parece incrível, mas funções aparentemente tão distantes se prestam a
"reunião". Além dos graus familiares em teoria e prática, existem outras abordagens para expandir uma função em uma série.
Nesta lição, conheceremos a série trigonométrica de Fourier, abordaremos a questão de sua convergência e soma e, é claro, analisaremos vários exemplos de expansão de funções em uma série de Fourier. Eu sinceramente queria chamar o artigo de “Série de Fourier para Leigos”, mas isso seria astuto, pois a resolução de problemas exigirá conhecimento de outras seções de análise matemática e alguma experiência prática. Portanto, o preâmbulo vai se assemelhar ao treinamento de astronautas =)
Primeiro, o estudo dos materiais da página deve ser abordado de forma excelente. Sonolento, descansado e sóbrio. Sem emoções fortes sobre uma perna de hamster quebrada e pensamentos obsessivos sobre as dificuldades da vida peixes de aquário. A série de Fourier não é difícil em termos de compreensão, no entanto, tarefas práticas requerem simplesmente concentração aumentada atenção - idealmente, você deve abandonar completamente os estímulos externos. A situação é agravada pelo fato de não haver uma maneira fácil de verificar a solução e a resposta. Assim, se sua saúde está abaixo da média, é melhor fazer algo mais simples. Verdade.
Em segundo lugar, antes de voar para o espaço, você precisa estudar o painel nave espacial. Vamos começar com os valores das funções que devem ser clicadas na máquina:
Para qualquer valor natural:
1) . E, de fato, a sinusóide "pisca" o eixo x através de cada "pi":
. No caso de valores negativos do argumento, o resultado, claro, será o mesmo: .
2). Mas nem todos sabiam disso. O cosseno "pi en" é o equivalente a uma "luz intermitente":
Um argumento negativo não muda o caso: 
.
Talvez o suficiente.
E em terceiro lugar, querido corpo de cosmonautas, você precisa ser capaz de ... integrar.
Em particular, com certeza colocar uma função sob um sinal diferencial, integrar por partes e estar em bons termos com Fórmula de Newton-Leibniz. Vamos começar os importantes exercícios pré-voo. Eu fortemente não recomendo pular, para que depois você não achate em gravidade zero:
Exemplo 1
Calcular integrais definidas
onde assume valores naturais.
Solução: a integração é realizada sobre a variável "x" e nesta etapa a variável discreta "en" é considerada uma constante. Em todas as integrais coloque a função sob o sinal da diferencial:
Uma versão curta da solução, que seria boa para filmar, é assim:
Acostumando:
Os quatro pontos restantes estão por conta própria. Tente tratar a tarefa com cuidado e organize as integrais de maneira curta. Exemplos de soluções no final da lição.
Depois de um exercício de QUALIDADE, vestimos os fatos espaciais
e se preparando para começar!
Vamos considerar uma função que determinado pelo menos no intervalo (e, possivelmente, em um intervalo maior). Se esta função for integrável no segmento , então ela pode ser expandida em uma função trigonométrica Séries de Fourier:
, onde estão os chamados Coeficientes de Fourier.
Neste caso, o número é chamado período de decomposição, e o número é decomposição de meia-vida.
Obviamente, no caso geral, a série de Fourier consiste em senos e cossenos: 
De fato, vamos escrevê-lo em detalhes:
O termo zero da série é geralmente escrito como .
Os coeficientes de Fourier são calculados usando as seguintes fórmulas: 
Entendo perfeitamente que novos termos ainda são obscuros para iniciantes no estudo do tema: período de decomposição, meio ciclo, Coeficientes de Fourier e outros. Não entre em pânico, não é comparável à emoção antes de uma caminhada espacial. Vamos descobrir tudo no exemplo mais próximo, antes de executá-lo, é lógico fazer perguntas práticas urgentes:
Expanda a função em uma série de Fourier. Além disso, muitas vezes é necessário desenhar um gráfico de uma função, um gráfico da soma de uma série, uma soma parcial e, no caso de fantasias sofisticadas de professores, fazer outra coisa.
Basicamente, você precisa encontrar Coeficientes de Fourier, ou seja, componha e calcule três integrais definidas.
Copie a forma geral da série de Fourier e as três fórmulas de trabalho em seu caderno. Fico muito feliz que alguns dos visitantes do site tenham um sonho de infância de se tornar um astronauta se tornando realidade bem na frente dos meus olhos =)
Exemplo 2
Expanda a função em uma série de Fourier no intervalo . Construa um gráfico, um gráfico da soma de uma série e uma soma parcial.
Solução: a primeira parte da tarefa é expandir a função em uma série de Fourier.
O começo é padrão, certifique-se de anotar isso:
Neste problema, o período de expansão , meio período .
Expandimos a função em uma série de Fourier no intervalo: 
Usando as fórmulas apropriadas, encontramos Coeficientes de Fourier. Agora precisamos compor e calcular três integrais definidas. Por conveniência, vou numerar os pontos:
1) A primeira integral é a mais simples, porém já requer olho e olho: 
2) Usamos a segunda fórmula:
Esta integral é bem conhecida e ele pega aos poucos: 
Quando encontrado usado método de colocar uma função sob um sinal diferencial.
Na tarefa em consideração, é mais conveniente usar imediatamente fórmula para integração por partes em uma integral definida 
:
Algumas notas técnicas. Primeiro, depois de aplicar a fórmula toda a expressão deve ser colocada entre colchetes grandes, pois há uma constante antes da integral original. Não vamos perdê-lo! Os parênteses podem ser abertos em qualquer passo seguinte, eu fiz isso no último turno. Na primeira "peça" 
mostramos extrema precisão na substituição, como você pode ver, a constante está fora do negócio e os limites de integração são substituídos no produto. Esta ação é marcada com colchetes. Bem, a integral do segundo "pedaço" da fórmula é bem conhecida por você da tarefa de treinamento ;-)
E o mais importante - a concentração máxima de atenção!
3) Estamos procurando o terceiro coeficiente de Fourier:
Obtém-se um relativo da integral anterior, que também é integrado por partes:
Esta instância é um pouco mais complicada, vou comentar as próximas etapas passo a passo: 
(1) A expressão inteira está entre colchetes grandes.. Eu não queria parecer chato, eles perdem a constante com muita frequência.
(2)B este caso Eu imediatamente abri aqueles grandes colchetes. Atenção especial
dedicamo-nos ao primeiro “pedaço”: o constante fuma à margem e não participa da substituição dos limites de integração ( e ) no produto . Tendo em vista a desordem do registro, é novamente aconselhável destacar essa ação entre colchetes. Com a segunda "peça" 
tudo é mais simples: aqui a fração apareceu depois de abrir colchetes grandes e a constante - como resultado da integração da familiar integral ;-)
(3) Nos colchetes, realizamos as transformações e, na integral à direita, substituímos os limites de integração.
(4) Retiramos o “pisca-pisca” dos colchetes: , após o que abrimos os colchetes internos: .
(5) Cancelamos 1 e -1 entre parênteses, fazemos simplificações finais.
Finalmente encontrei todos os três coeficientes de Fourier: 
Substitua-os na fórmula 
:
Não se esqueça de dividir ao meio. Na última etapa, a constante ("menos dois"), que não depende de "en", é retirada da soma.
Assim, obtivemos a expansão da função em série de Fourier no intervalo: 
Estudemos a questão da convergência da série de Fourier. Vou explicar a teoria em particular teorema de Dirichlet, literalmente "nos dedos", portanto, se você precisar de formulações estritas, consulte um livro de cálculo (por exemplo, o 2º volume de Bohan; ou o 3º volume de Fichtenholtz, mas é mais difícil nele).
Na segunda parte da tarefa, é necessário desenhar um gráfico, um gráfico de soma de séries e um gráfico de soma parcial.
O gráfico da função é o usual linha reta no plano, que é desenhado com uma linha pontilhada preta: 
Nós lidamos com a soma da série. Como você sabe, séries funcionais convergem para funções. No nosso caso, a série de Fourier construída 
para qualquer valor de "x" converge para a função mostrada em vermelho. esta função resiste pausas de 1º tipo em pontos, mas também definidos neles (pontos vermelhos no desenho)
Nesse caminho: 
. É fácil ver que ela difere marcadamente da função original, razão pela qual na notação 
um til é usado em vez de um sinal de igual.
Vamos estudar um algoritmo pelo qual é conveniente construir a soma de uma série.
No intervalo central, a série de Fourier converge para a própria função (o segmento vermelho central coincide com a linha pontilhada preta da função linear).
Agora vamos falar um pouco sobre a natureza da expansão trigonométrica considerada. Séries de Fourier 
inclui apenas funções periódicas (constante, senos e cossenos), então a soma da série 
também é uma função periódica.
O que isso significa em nosso exemplo específico? E isso significa que a soma da série 
–necessariamente periódica e o segmento vermelho do intervalo deve ser repetido infinitamente à esquerda e à direita.
Acho que agora o significado da frase "período de decomposição" finalmente ficou claro. Simplificando, toda vez que a situação se repete de novo e de novo.
Na prática, geralmente é suficiente representar três períodos de decomposição, como é feito no desenho. Bem, e mais "tocos" de períodos vizinhos - para deixar claro que o gráfico continua.
De particular interesse são pontos de descontinuidade de 1º tipo. Nesses pontos, a série de Fourier converge para valores isolados, que se localizam exatamente no meio do "salto" da descontinuidade (pontos vermelhos no desenho). Como encontrar a ordenada desses pontos? Primeiro, vamos encontrar a ordenada do "piso superior": para isso, calculamos o valor da função no ponto mais à direita do período de expansão central: . Para calcular a ordenada do “piso inferior”, a maneira mais fácil é pegar o valor mais à esquerda do mesmo período: 
. A ordenada do valor médio é a média aritmética da soma do "superior e inferior": . Bom é o fato de que ao construir um desenho, você verá imediatamente se o meio está calculado corretamente ou incorretamente.
Vamos construir uma soma parcial da série e ao mesmo tempo repetir o significado do termo "convergência". O motivo é conhecido da lição sobre a soma da série numérica. Vamos descrever nossa riqueza em detalhes:
Para fazer uma soma parcial, você precisa anotar zero + mais dois termos da série. Aquilo é,
No desenho, o gráfico da função é mostrado em verde e, como você pode ver, envolve a soma total com bastante precisão. Se considerarmos uma soma parcial de cinco termos da série, o gráfico dessa função aproximará as linhas vermelhas com ainda mais precisão; se houver cem termos, a “serpente verde” se fundirá completamente com os segmentos vermelhos, etc. Assim, a série de Fourier converge para sua soma.
É interessante notar que qualquer soma parcial é função contínua, mas a soma total da série ainda é descontínua.
Na prática, não é incomum construir um gráfico de soma parcial. Como fazer isso? No nosso caso, é necessário considerar a função no segmento, calcular seus valores nas extremidades do segmento e nos pontos intermediários (quanto mais pontos você considerar, mais preciso será o gráfico). Então você deve marcar esses pontos no desenho e desenhar cuidadosamente um gráfico no período , e depois “replicá-lo” em intervalos adjacentes. De que outra forma? Afinal, a aproximação também é uma função periódica ... ... seu gráfico de alguma forma me lembra um ritmo cardíaco uniforme no visor de um dispositivo médico.
Claro, não é muito conveniente fazer a construção, pois é preciso ter muito cuidado, mantendo uma precisão não inferior a meio milímetro. No entanto, agradarei aos leitores que estão em desacordo com o desenho - em uma tarefa "real", nem sempre é necessário fazer um desenho, em algum lugar em 50% dos casos é necessário expandir a função para uma série de Fourier e isso é isto.
Depois de concluir o desenho, concluímos a tarefa:
Responda: 
Em muitas tarefas, a função sofre ruptura de 1ª espécie logo no período de decomposição:
Exemplo 3
Expanda em uma série de Fourier a função dada no intervalo. Desenhe um gráfico da função e a soma total da série.
A função proposta é dada por partes (e, lembre-se, apenas no segmento) e suportar ruptura de 1ª espécie no ponto . É possível calcular os coeficientes de Fourier? Sem problemas. As partes esquerda e direita da função são integráveis em seus intervalos, portanto, as integrais em cada uma das três fórmulas devem ser representadas como a soma de duas integrais. Vejamos, por exemplo, como isso é feito para um coeficiente zero:
A segunda integral acabou sendo igual a zero, o que reduziu o trabalho, mas nem sempre é assim.
Dois outros coeficientes de Fourier são escritos de forma semelhante.
Como exibir a soma de uma série? No intervalo esquerdo, desenhamos um segmento de linha reta e no intervalo - um segmento de linha reta (destaque a seção do eixo em negrito-negrito). Ou seja, no intervalo de expansão, a soma da série coincide com a função em todos os lugares, exceto em três pontos "ruins". No ponto de descontinuidade da função, a série de Fourier converge para um valor isolado, que se localiza exatamente no meio do “salto” da descontinuidade. Não é difícil vê-lo oralmente: limite da mão esquerda:, limite da mão direita: 
e, obviamente, a ordenada do ponto médio é 0,5.
Devido à periodicidade da soma , a imagem deve ser “multiplicada” em períodos vizinhos, em particular, retratar a mesma coisa nos intervalos e . Neste caso, nos pontos, a série de Fourier converge para os valores medianos.
Na verdade, não há nada de novo aqui.
Tente resolver esse problema sozinho. Uma amostra aproximada de design fino e desenho no final da lição.
Para um período de expansão arbitrário, onde "el" é qualquer número positivo, as fórmulas para a série de Fourier e os coeficientes de Fourier diferem em um argumento de seno e cosseno um pouco mais complicado:
Se , obtemos as fórmulas para o intervalo com o qual começamos.
O algoritmo e os princípios para resolver o problema são totalmente preservados, mas a complexidade técnica dos cálculos aumenta:
Exemplo 4
Expanda a função em uma série de Fourier e plote a soma. 
Solução: de fato, um análogo do Exemplo No. 3 com ruptura de 1ª espécie no ponto . Neste problema, o período de expansão , meio período . A função é definida apenas no meio-intervalo , mas isso não muda as coisas - é importante que ambas as partes da função sejam integráveis.
Vamos expandir a função em uma série de Fourier:
Como a função é descontínua na origem, cada coeficiente de Fourier obviamente deve ser escrito como a soma de duas integrais:
1) Vou escrever a primeira integral o mais detalhadamente possível:
2) Observe cuidadosamente a superfície da lua:
segunda integral pegue em partes:
O que você deve prestar muita atenção depois de abrirmos a continuação da solução com um asterisco?
Primeiro, não perdemos a primeira integral 
, onde executamos imediatamente colocando sob o sinal do diferencial. Em segundo lugar, não se esqueça da constante malfadada antes dos colchetes grandes e não se confunda com sinais ao usar a fórmula 
. Colchetes grandes, afinal, é mais conveniente abrir imediatamente na próxima etapa.
O resto é uma questão de técnica, apenas a experiência insuficiente na resolução de integrais pode causar dificuldades.
Sim, não foi à toa que os eminentes colegas do matemático francês Fourier ficaram indignados - como ele ousou decompor funções em séries trigonométricas ?! =) A propósito, provavelmente todos estão interessados no significado prático da tarefa em questão. O próprio Fourier trabalhou modelo matemático condutividade térmica, e mais tarde a série que leva seu nome começou a ser usada para estudar muitos processos periódicos, aparentemente invisíveis no mundo circundante. Agora, aliás, me peguei pensando que não foi por acaso que comparei o gráfico do segundo exemplo com um ritmo cardíaco periódico. Quem quiser pode se familiarizar com aplicação prática transformada de Fourier de fontes de terceiros. ... Embora seja melhor não - será lembrado como Primeiro Amor =)
3) Dados os elos fracos repetidamente mencionados, lidamos com o terceiro coeficiente:
Integrando por partes: 
Substituímos os coeficientes de Fourier encontrados na fórmula 
, não esquecendo de dividir o coeficiente zero pela metade:
Vamos traçar a soma da série. Vamos repetir brevemente o procedimento: no intervalo construímos uma linha e no intervalo - uma linha. Com valor zero de "x", colocamos um ponto no meio do "salto" do gap e "replicamos" o gráfico para os períodos vizinhos: 
Nas "junções" dos períodos, a soma também será igual aos pontos médios do "salto" do gap.
Preparar. Lembro que a própria função é definida condicionalmente apenas no meio intervalo e, obviamente, coincide com a soma da série nos intervalos
Responda:
Às vezes, uma dada função por partes também é contínua no período de expansão. O exemplo mais simples: 
. Solução (Ver Bohan Volume 2)é o mesmo que nos dois exemplos anteriores: apesar continuidade da função no ponto , cada coeficiente de Fourier é expresso como a soma de duas integrais.
No intervalo de separação pontos de descontinuidade de 1º tipo e/ou pontos de "junção" do gráfico podem ser mais (dois, três e, em geral, qualquer final quantia). Se uma função é integrável em todas as partes, ela também é expansível em uma série de Fourier. Mas, por experiência prática, não me lembro de tal lata. No entanto, existem tarefas mais difíceis do que apenas consideradas, e no final do artigo para todos há links para a série Fourier de maior complexidade.
Enquanto isso, vamos relaxar, recostados em nossas cadeiras e contemplando a imensidão das estrelas:
Exemplo 5
Expanda a função em uma série de Fourier no intervalo e plote a soma da série.
Nesta tarefa, a função contínuo no semi-intervalo de decomposição, o que simplifica a solução. Tudo é muito parecido com o Exemplo #2. Você não pode fugir da nave - você terá que decidir =) Exemplo de design no final da aula, o cronograma está anexado.
Com funções pares e ímpares, o processo de resolução do problema é visivelmente simplificado. E é por isso. Voltemos à expansão da função em série de Fourier em um período de "dois pi" 
e período arbitrário "duas cervejas" 
.
Vamos supor que nossa função seja par. O termo geral da série, como você pode ver, contém cossenos pares e senos ímpares. E se decompormos uma função PAR, então por que precisamos de senos ímpares?! Vamos redefinir o coeficiente desnecessário: .
Nesse caminho, uma função par se expande em uma série de Fourier apenas em cossenos:
Porque o integrais de funções pares sobre um segmento de integração simétrico em relação a zero pode ser duplicado, então o resto dos coeficientes de Fourier também são simplificados.
Para extensão: 
Para um intervalo arbitrário: 
Exemplos de livros didáticos encontrados em quase todos os livros didáticos de cálculo incluem expansões de funções pares 
. Além disso, eles se encontraram repetidamente em minha prática pessoal:
Exemplo 6
Dada uma função. Requeridos:
1) expanda a função em uma série de Fourier com período , onde é um número positivo arbitrário;
2) escreva a expansão no intervalo, construa uma função e represente graficamente a soma total da série.
Solução: no primeiro parágrafo propõe-se resolver o problema em visão geral e é muito conveniente! Haverá uma necessidade - basta substituir seu valor.
1) Neste problema, o período de expansão , meio período . No decorrer de outras ações, em particular durante a integração, "el" é considerado uma constante
A função é par, o que significa que ela se expande em uma série de Fourier apenas em cossenos: 
.
Os coeficientes de Fourier são procurados pelas fórmulas 
. Preste atenção às suas vantagens absolutas. Primeiro, a integração é realizada no segmento positivo da expansão, o que significa que nos livramos do módulo com segurança 
, considerando apenas "x" de duas peças. E, em segundo lugar, a integração é visivelmente simplificada.
Dois: 
Integrando por partes:
Nesse caminho:
, enquanto a constante , que não depende de "en", é retirada da soma.
Responda: 
2) Escrevemos a expansão no intervalo, para isso substituímos o valor desejado do meio período na fórmula geral:
A série de Fourier de uma função periódica par f(x) com período 2p contém apenas termos de cosseno (isto é, não contém termos de seno) e pode incluir um termo constante. Consequentemente,
onde são os coeficientes da série de Fourier,
A série de Fourier de uma função periódica ímpar f (x) com um período de 2p contém apenas termos com senos (ou seja, não contém termos com cossenos).
Consequentemente,
onde são os coeficientes da série de Fourier,
Se uma função é definida para um intervalo, digamos 0 a p, e não apenas 0 a 2p, ela pode ser expandida em uma série apenas em termos de senos ou apenas em termos de cossenos. A série de Fourier resultante é chamada ao lado Fourier no meio ciclo.
Se você deseja obter uma decomposição Fourier no meio ciclo sobre cossenos funções f(x) no intervalo de 0 a p, então é necessário compor uma função periódica par. Na fig. abaixo está a função f(x) =x, construída no intervalo de x=0 a x=p. Como a função par é simétrica em relação ao eixo f (x), desenhamos a linha AB, conforme mostrado na Fig. abaixo de. Se assumirmos que fora do intervalo considerado, a forma triangular resultante é periódica com um período de 2p, então o gráfico final tem a forma, display. na fig. abaixo de. Como é necessário obter a expansão de Fourier em cossenos, como antes, calculamos os coeficientes de Fourier a o e an
Se você precisa obter decomposição Fourier no meio ciclo sobre seios da face funções f(x) no intervalo de 0 a p, então é necessário compor uma função periódica ímpar. Na fig. abaixo está a função f(x)=x construída no intervalo de x=0 a x=p. Como a função ímpar é simétrica em relação à origem, construímos a linha CD, conforme mostrado na Fig.
Se assumirmos que fora do intervalo considerado, o sinal dente de serra recebido é periódico com período de 2p, então o gráfico final tem a forma mostrada na Fig. Como é necessário obter a expansão de Fourier em um meio ciclo em termos de senos, como antes, calculamos o coeficiente de Fourier. b
Como inserir fórmulas matemáticas no site?
Se você precisar adicionar uma ou duas fórmulas matemáticas a uma página da Web, a maneira mais fácil de fazer isso é conforme descrito no artigo: as fórmulas matemáticas são facilmente inseridas no site na forma de imagens que o Wolfram Alpha gera automaticamente. Além da simplicidade, esse método universal ajudará a melhorar a visibilidade do site em motores de busca. Funciona há muito tempo (e acho que funcionará para sempre), mas está moralmente desatualizado.
Se você estiver constantemente usando fórmulas matemáticas em seu site, recomendo que você use MathJax, uma biblioteca JavaScript especial que exibe notação matemática em navegadores da Web usando marcação MathML, LaTeX ou ASCIIMathML.
Existem duas maneiras de começar a usar o MathJax: (1) usando um código simples, você pode conectar rapidamente um script MathJax ao seu site, que será carregado automaticamente de um servidor remoto no momento certo (lista de servidores); (2) carregue o script MathJax de um servidor remoto para o seu servidor e conecte-o a todas as páginas do seu site. O segundo método é mais complexo e demorado e permitirá que você acelere o carregamento das páginas do seu site, e se o servidor MathJax pai ficar temporariamente indisponível por algum motivo, isso não afetará seu próprio site de forma alguma. Apesar dessas vantagens, optei pelo primeiro método, por ser mais simples, rápido e não exigir habilidades técnicas. Siga meu exemplo e em 5 minutos você poderá usar todos os recursos do MathJax em seu site.
Você pode conectar o script da biblioteca MathJax de um servidor remoto usando duas opções de código retiradas do site principal do MathJax ou da página de documentação:
Uma dessas opções de código precisa ser copiada e colada no código da sua página da web, de preferência entre as tags
e ou logo após a tag . De acordo com a primeira opção, o MathJax carrega mais rápido e torna a página menos lenta. Mas a segunda opção rastreia e carrega automaticamente as versões mais recentes do MathJax. Se você inserir o primeiro código, ele precisará ser atualizado periodicamente. Se você colar o segundo código, as páginas carregarão mais lentamente, mas você não precisará monitorar constantemente as atualizações do MathJax.A maneira mais fácil de conectar o MathJax é no Blogger ou WordPress: no painel de controle do site, adicione um widget projetado para inserir código JavaScript de terceiros, copie a primeira ou a segunda versão do código de carregamento acima e coloque o widget mais próximo de o início do modelo (aliás, isso não é necessário , pois o script MathJax é carregado de forma assíncrona). Isso é tudo. Agora aprenda a sintaxe de marcação MathML, LaTeX e ASCIIMathML e você estará pronto para incorporar fórmulas matemáticas em suas páginas da web.
Qualquer fractal é construído de acordo com uma determinada regra, que é aplicada consistentemente um número ilimitado de vezes. Cada um desses tempos é chamado de iteração.
O algoritmo iterativo para a construção de uma esponja Menger é bastante simples: o cubo original com lado 1 é dividido por planos paralelos às suas faces em 27 cubos iguais. Um cubo central e 6 cubos adjacentes a ele ao longo das faces são removidos dele. Acontece um conjunto composto por 20 cubos menores restantes. Fazendo o mesmo com cada um desses cubos, obtemos um conjunto composto por 400 cubos menores. Continuando esse processo indefinidamente, obtemos a esponja Menger.
A série de Fourier é uma representação de uma função tomada arbitrariamente com um período específico como uma série. Em termos gerais, essa solução é chamada de decomposição de um elemento em base ortogonal. A expansão de funções em uma série de Fourier é uma ferramenta bastante poderosa para resolver vários problemas devido às propriedades dessa transformação ao integrar, diferenciar, bem como deslocar uma expressão em um argumento e convolução.
Uma pessoa que não conhece matemática superior, assim como com os trabalhos do cientista francês Fourier, muito provavelmente, não vai entender o que são essas “séries” e para que servem. Entretanto, essa transformação se tornou bastante densa em nossas vidas. É usado não apenas por matemáticos, mas também por físicos, químicos, médicos, astrônomos, sismólogos, oceanógrafos e muitos outros. Vejamos também mais de perto as obras do grande cientista francês, que fez uma descoberta à frente de seu tempo.
A série de Fourier é um dos métodos (juntamente com a análise e outros). Esse processo ocorre toda vez que uma pessoa ouve algum som. Nosso ouvido converte automaticamente partículas elementares em um meio elástico são decompostos em linhas (ao longo do espectro) de valores sucessivos do nível de intensidade para tons de diferentes alturas. Em seguida, o cérebro transforma esses dados em sons familiares para nós. Tudo isso acontece além do nosso desejo ou consciência, por si só, mas para entender esses processos, serão necessários vários anos para estudar matemática superior.
A transformada de Fourier pode ser realizada por métodos analíticos, numéricos e outros. As séries de Fourier referem-se à forma numeral de decompor qualquer processo oscilatório - das marés oceânicas e ondas de luz aos ciclos da atividade solar (e outros objetos astronômicos). Usando essas técnicas matemáticas, é possível analisar funções, representando quaisquer processos oscilatórios como uma série de componentes senoidais que vão do mínimo ao máximo e vice-versa. A transformada de Fourier é uma função que descreve a fase e a amplitude das senoides correspondentes a uma frequência específica. Este processo pode ser usado para resolver equações muito complexas que descrevem processos dinâmicos que ocorrem sob a influência de energia térmica, luminosa ou elétrica. Além disso, as séries de Fourier permitem isolar os componentes constantes em sinais oscilatórios complexos, o que permite interpretar corretamente as observações experimentais obtidas em medicina, química e astronomia.
O pai fundador desta teoria é o matemático francês Jean Baptiste Joseph Fourier. Esta transformação foi posteriormente nomeada em sua homenagem. Inicialmente, o cientista aplicou seu método para estudar e explicar os mecanismos de condução de calor - a propagação do calor em sólidos. Fourier sugeriu que a distribuição irregular original pode ser decomposta nas sinusóides mais simples, cada uma das quais terá sua própria temperatura mínima e máxima, bem como sua própria fase. Nesse caso, cada um desses componentes será medido do mínimo ao máximo e vice-versa. A função matemática que descreve os picos superiores e inferiores da curva, bem como a fase de cada um dos harmônicos, é chamada de transformada de Fourier da expressão da distribuição de temperatura. O autor da teoria reduziu a função de distribuição geral, que é difícil de descrever matematicamente, a uma série muito conveniente de cosseno e seno, que se somam para dar a distribuição original.
Os contemporâneos do cientista - os principais matemáticos do início do século XIX - não aceitaram essa teoria. A principal objeção foi a afirmação de Fourier de que uma função descontínua descrevendo uma linha reta ou uma curva descontínua pode ser representada como uma soma de expressões senoidais que são contínuas. Como exemplo, considere o "passo" de Heaviside: seu valor é zero à esquerda do intervalo e um à direita. Esta função descreve a dependência da corrente elétrica na variável de tempo quando o circuito é fechado. Os contemporâneos da teoria da época nunca haviam encontrado situação similar, quando a expressão descontínua seria descrita por uma combinação de funções convencionais contínuas, como exponencial, senoidal, linear ou quadrática.
Afinal, se o matemático estava certo em suas afirmações, então, ao somar a infinita série trigonométrica de Fourier, pode-se obter uma representação exata da expressão passo a passo, mesmo que ela tenha muitos passos semelhantes. No início do século XIX, tal afirmação parecia absurda. Mas, apesar de todas as dúvidas, muitos matemáticos ampliaram o escopo do estudo desse fenômeno, levando-o para além do escopo dos estudos de condutividade térmica. No entanto, a maioria dos cientistas continuou a ser atormentada pela questão: "Pode a soma de uma série senoidal convergir para valor exato função descontínua?"
A questão da convergência é levantada sempre que é necessário somar séries infinitas de números. Para entender esse fenômeno, considere um exemplo clássico. Você pode alcançar a parede se cada passo sucessivo tiver metade do tamanho do anterior? Suponha que você esteja a dois metros do gol, o primeiro passo o aproxima da metade do caminho, o próximo da marca de três quartos e, após o quinto passo, você cobrirá quase 97% do caminho. No entanto, não importa quantos passos você dê, você não alcançará o objetivo pretendido em um sentido matemático estrito. Usando cálculos numéricos, pode-se mostrar que, no final, é possível aproximar-se de uma distância arbitrariamente pequena. Esta prova equivale a demonstrar que o valor total de um meio, um quarto, etc. tenderá para um.
ré essa questão aumentou no final do século XIX, quando as séries de Fourier foram usadas para prever a intensidade do fluxo e refluxo. Nessa época, um dispositivo foi inventado por Lord Kelvin, que é um dispositivo de computação analógica que permitia aos marinheiros da frota militar e mercante rastrear esse um fenômeno natural. Esse mecanismo determinava os conjuntos de fases e amplitudes de uma tabela de alturas de maré e seus correspondentes momentos de tempo, cuidadosamente medidos em um determinado porto durante o ano. Cada parâmetro era um componente senoidal da expressão da altura da maré e era um dos componentes regulares. Os resultados das medições foram inseridos na calculadora de Lord Kelvin, que sintetizou uma curva que previu a altura da água em função do tempo para o próximo ano. Muito em breve curvas semelhantes foram traçadas para todos os portos do mundo.
Naquela época, parecia óbvio que um preditor de maremotos com grande quantidade elementos da conta podem calcular um grande número de fases e amplitudes e assim fornecer previsões mais precisas. No entanto, verificou-se que essa regularidade não é observada nos casos em que a expressão de maré a ser sintetizada continha um salto acentuado, ou seja, era descontínua. Caso os dados sejam inseridos no dispositivo a partir da tabela de momentos de tempo, ele calcula vários coeficientes de Fourier. A função original é restaurada graças aos componentes senoidais (de acordo com os coeficientes encontrados). A discrepância entre a expressão original e restaurada pode ser medida em qualquer ponto. Ao realizar cálculos e comparações repetidas, pode-se ver que o valor do maior erro não diminui. No entanto, eles estão localizados na região correspondente ao ponto de descontinuidade e tendem a zero em qualquer outro ponto. Em 1899, esse resultado foi confirmado teoricamente por Joshua Willard Gibbs, da Universidade de Yale.
A análise de Fourier não é aplicável a expressões contendo um número infinito de rajadas em um determinado intervalo. Em geral, série de Fourier, se a função original é representada pelo resultado de um real dimensão física, sempre convergem. Questões sobre a convergência desse processo para classes específicas de funções levaram ao surgimento de novas seções na matemática, por exemplo, a teoria das funções generalizadas. Está associado a nomes como L. Schwartz, J. Mikusinsky e J. Temple. Dentro da estrutura desta teoria, uma clara e precisa base teórica sob expressões como a função delta de Dirac (descreve uma região de uma única área concentrada em uma vizinhança infinitesimal de um ponto) e o "passo" de Heaviside. Graças a este trabalho, a série de Fourier tornou-se aplicável à resolução de equações e problemas em que aparecem conceitos intuitivos: uma carga pontual, uma massa pontual, dipolos magnéticos e também uma carga concentrada em uma viga.
As séries de Fourier, de acordo com os princípios da interferência, começam com a decomposição de formas complexas em formas mais simples. Por exemplo, uma mudança no fluxo de calor é explicada por sua passagem por vários obstáculos de um material isolante de calor. forma irregular ou uma mudança na superfície da terra - um terremoto, uma mudança na órbita de um corpo celeste - a influência dos planetas. Como regra, equações semelhantes descrevendo sistemas clássicos simples são resolvidas elementarmente para cada onda individual. Fourier mostrou que soluções simples também podem ser resumidos para obter soluções para problemas mais complexos. Expresso na linguagem da matemática, a série de Fourier é uma técnica para representar uma expressão como a soma dos harmônicos - cosseno e sinusóides. É por isso esta análise também conhecido como "análise harmônica".
Antes da criação da tecnologia de computador, a técnica de Fourier era melhor arma no arsenal dos cientistas ao trabalhar com a natureza ondulatória do nosso mundo. Série de Fourier em forma complexa permite que você decida não apenas tarefas simples, que são passíveis de aplicação direta das leis da mecânica newtoniana, mas também equações fundamentais. A maioria das descobertas da ciência newtoniana no século XIX foram possíveis apenas pela técnica de Fourier.
Com o desenvolvimento dos computadores, as transformadas de Fourier elevaram-se a um nível qualitativamente novo. Esta técnica está firmemente arraigada em quase todas as áreas da ciência e tecnologia. Um exemplo é um sinal de áudio e vídeo digital. Sua realização só foi possível graças à teoria desenvolvida por um matemático francês no início do século XIX. Assim, a série de Fourier na forma complexa possibilitou um avanço no estudo espaço sideral. Além disso, isso influenciou o estudo da física de materiais semicondutores e plasma, acústica de microondas, oceanografia, radar e sismologia.
Em matemática, uma série de Fourier é uma forma de representar funções complexas a soma das mais simples. NO casos comuns o número de tais expressões pode ser infinito. Além disso, quanto mais seu número for levado em consideração no cálculo, mais preciso será o resultado final. Mais frequentemente usado como o mais simples funções trigonométricas cosseno ou seno. Nesse caso, as séries de Fourier são chamadas de trigonométricas, e a solução de tais expressões é chamada de expansão do harmônico. Este método desempenha um papel importante na matemática. Em primeiro lugar, a série trigonométrica fornece um meio para a imagem, bem como o estudo das funções, é o principal aparato da teoria. Além disso, permite resolver uma série de problemas de física matemática. Finalmente, esta teoria contribuiu para o desenvolvimento e deu vida a uma série de seções muito importantes ciência matemática(a teoria das integrais, a teoria das funções periódicas). Além disso, serviu de ponto de partida para o desenvolvimento das seguintes funções de uma variável real e também marcou o início da análise harmônica.
