O posto de uma matriz é um fator importante característica numérica. O problema mais característico que requer encontrar o posto de uma matriz é verificar a compatibilidade de um sistema de lineares equações algébricas. Neste artigo, daremos o conceito de classificação de uma matriz e consideraremos métodos para encontrá-la. Para uma melhor assimilação do material, analisaremos detalhadamente as soluções de diversos exemplos.
Navegação da página.
Antes de expressar a definição do posto de uma matriz, deve-se ter um bom entendimento do conceito de menor, e encontrar os menores de uma matriz implica a capacidade de calcular o determinante. Portanto, recomendamos, se necessário, relembrar a teoria do artigo, métodos para encontrar o determinante da matriz, propriedades do determinante.
Tome uma matriz A de ordem . Seja k algum número natural, não excedendo o menor dos números m e n , ou seja, .
Definição.
Ordem k-ésima menor A matriz A é o determinante da matriz quadrada de ordem , composta pelos elementos da matriz A, que estão em k linhas e k colunas pré-selecionadas, e a localização dos elementos da matriz A é preservada.
Em outras palavras, se excluirmos (p–k) linhas e (n–k) colunas na matriz A e formarmos uma matriz a partir dos elementos restantes, preservando o arranjo dos elementos da matriz A, então o determinante da matriz resultante é um menor de ordem k da matriz A.
Vejamos a definição de uma matriz menor usando um exemplo.
Considere a matriz 
.
Vamos escrever vários menores de primeira ordem desta matriz. Por exemplo, se escolhermos a terceira linha e a segunda coluna da matriz A, então nossa escolha corresponde a um menor de primeira ordem 
. Em outras palavras, para obter esse menor, riscamos a primeira e segunda linhas, bem como a primeira, terceira e quarta colunas da matriz A, e fizemos o determinante do elemento restante. Se escolhermos a primeira linha e a terceira coluna da matriz A, obtemos um menor 
.
Vamos ilustrar o procedimento para obtenção dos considerados menores de primeira ordem 
e 
.
Assim, os menores de primeira ordem de uma matriz são os próprios elementos da matriz.
Mostremos vários menores de segunda ordem. Selecione duas linhas e duas colunas. Por exemplo, pegue a primeira e a segunda linhas e a terceira e a quarta colunas. Com esta escolha, temos um menor de segunda ordem 
. Este menor também pode ser formado pela exclusão da terceira linha, primeira e segunda colunas da matriz A.
Outro menor de segunda ordem da matriz A é .
Vamos ilustrar a construção desses menores de segunda ordem 
e 
.
Os menores de terceira ordem da matriz A podem ser encontrados de forma similar. Como existem apenas três linhas na matriz A, selecionamos todas elas. Se selecionarmos as três primeiras colunas para essas linhas, obteremos um menor da terceira ordem 
Também pode ser construído excluindo a última coluna da matriz A.
Outro menor de terceira ordem é 
obtido deletando a terceira coluna da matriz A.
Aqui está um desenho mostrando a construção desses menores de terceira ordem 
e 
.
Para uma dada matriz A, não existem menores de ordem superior à terça, pois .
Quantos menores de ordem k da matriz A de ordem existem?
O número de menores de ordem k pode ser calculado como , onde 
e 
- o número de combinações de p a k e de n a k, respectivamente.
Como construir todos os menores de ordem k da matriz A de ordem p em n?
Precisamos de um conjunto de números de linhas da matriz e um conjunto de números de colunas. Gravando tudo combinações de p elementos por k(corresponderão às linhas selecionadas da matriz A ao construir um menor de ordem k). Para cada combinação de números de linha, adicionamos sequencialmente todas as combinações de n elementos por k números de coluna. Esses conjuntos de combinações de números de linhas e números de colunas da matriz A ajudarão a compor todos os menores de ordem k.
Vamos dar um exemplo.
Exemplo.
Encontre todos os menores de segunda ordem da matriz.
Solução.
Como a ordem da matriz original é 3 por 3, o total de menores de segunda ordem será 
.
Vamos anotar todas as combinações de números de 3 a 2 linhas da matriz A: 1, 2; 1, 3 e 2, 3. Todas as combinações de números de coluna 3 por 2 são 1, 2 ; 1, 3 e 2, 3.
Pegue a primeira e a segunda linhas da matriz A. Selecionando a primeira e a segunda colunas para essas linhas, a primeira e a terceira colunas, a segunda e a terceira colunas, obtemos, respectivamente, os menores 
Para a primeira e terceira linhas, com uma escolha similar de colunas, temos 
Resta adicionar a primeira e segunda, primeira e terceira, segunda e terceira colunas à segunda e terceira linhas: 
Assim, todos os nove menores de segunda ordem da matriz A são encontrados.
Agora podemos prosseguir para determinar o posto da matriz.
Definição.
Classificação da matrizé a ordem mais alta da matriz menor não nula.
O posto da matriz A é denotado como Posto(A). Você também pode ver as designações Rg(A) ou Rang(A) .
A partir das definições do posto de uma matriz e do menor de uma matriz, podemos concluir que o posto de uma matriz zero é igual a zero e o posto de uma matriz diferente de zero é pelo menos um.
Assim, o primeiro método para encontrar o posto de uma matriz é método de enumeração menor. Este método é baseado na determinação do posto da matriz.
Precisamos encontrar o posto de uma matriz A de ordem .
Descreva resumidamente algoritmo solução deste problema pelo método de enumeração de menores.
Se houver pelo menos um elemento da matriz diferente de zero, o posto da matriz será pelo menos igual a um (já que existe um menor de primeira ordem que não é igual a zero).
Em seguida, iteramos sobre os menores de segunda ordem. Se todos os menores de segunda ordem forem iguais a zero, o posto da matriz será igual a um. Se existir pelo menos um menor de segunda ordem diferente de zero, então passamos para a enumeração de menores de terceira ordem, e o posto da matriz é pelo menos igual a dois.
Da mesma forma, se todos os menores de terceira ordem forem zero, o posto da matriz será dois. Se houver pelo menos um menor de terceira ordem diferente de zero, o posto da matriz é de pelo menos três e procedemos à enumeração dos menores de quarta ordem.
Observe que o posto de uma matriz não pode exceder o menor de p e n.
Exemplo.
Encontrar o posto de uma matriz 
.
Solução.
Como a matriz é diferente de zero, sua classificação não é menor que um.
Menor de segunda ordem 
é diferente de zero, portanto, o posto da matriz A é pelo menos dois. Passamos à enumeração dos menores de terceira ordem. Todos eles 
coisas. 
Todos os menores de terceira ordem são iguais a zero. Portanto, o posto da matriz é dois.
Responda:
Classificação(A) = 2 .
Existem outros métodos para encontrar o posto de uma matriz que permitem obter o resultado com menos trabalho computacional.
Um desses métodos é método menor de franja.
Vamos lidar com a noção de um menor limítrofe.
Diz-se que o menor M ok de (k+1)ésima ordem da matriz A circunda o menor M de ordem k da matriz A se a matriz correspondente ao menor M ok "contiver" a matriz correspondente ao menor M.
Em outras palavras, a matriz correspondente ao menor de borda M é obtida a partir da matriz correspondente ao menor de borda M ok deletando os elementos de uma linha e uma coluna.
Por exemplo, considere a matriz 
e tomar um menor de segunda ordem. Vamos anotar todos os menores limítrofes: 
O método dos menores limítrofes é justificado pelo seguinte teorema (apresentamos sua formulação sem demonstração).
Teorema.
Se todos os menores que fazem fronteira com o menor de ordem k de uma matriz A de ordem p por n são iguais a zero, então todos os menores de ordem (k + 1) da matriz A são iguais a zero.
Assim, para encontrar o posto de uma matriz, não é necessário enumerar todos os menores que são suficientemente limítrofes. O número de menores que fazem fronteira com o menor de ordem k da matriz A de ordem é encontrado pela fórmula 
. Observe que não há mais menores na borda do menor de ordem k da matriz A do que menores de ordem (k + 1) na matriz A . Portanto, na maioria dos casos, usar o método de fronteira de menores é mais lucrativo do que simplesmente enumerar todos os menores.
Prossigamos para encontrar o posto de uma matriz pelo método de franjas menores. Descreva resumidamente algoritmo este método.
Se a matriz A for diferente de zero, consideramos qualquer elemento da matriz A que seja diferente de zero como um menor de primeira ordem. Consideramos seus limítrofes menores. Se todos forem iguais a zero, o posto da matriz é igual a um. Se houver pelo menos um menor limítrofe diferente de zero (sua ordem é igual a dois), então passamos à consideração de seus limítrofes menores. Se todos forem zero, então Rank(A) = 2 . Se pelo menos um menor limítrofe for diferente de zero (sua ordem é igual a três), então consideramos seus menores limítrofes. E assim por diante. Como resultado, Rank(A) = k se todos os menores limítrofes da (k + 1)ª ordem da matriz A forem iguais a zero, ou Rank(A) = min(p, n) se existir um diferente de zero menor beirando um menor de ordem (min( p, n) – 1) .
Vamos analisar o método de bordar menores para encontrar o posto de uma matriz usando um exemplo.
Exemplo.
Encontrar o posto de uma matriz 
pelo método dos menores limítrofes.
Solução.
Como o elemento a 1 1 da matriz A é diferente de zero, nós o tomamos como um menor de primeira ordem. Vamos começar a procurar por um menor limítrofe diferente de zero: 
Um menor de segunda ordem de borda diferente de zero é encontrado. Enumeremos seus menores limítrofes (suas 
coisas): 
Todos os menores que fazem fronteira com o menor de segunda ordem são iguais a zero, portanto, o posto da matriz A é igual a dois.
Responda:
Classificação(A) = 2 .
Exemplo.
Encontrar o posto de uma matriz 
com a ajuda de menores fronteiriços.
Solução.
Como um menor diferente de zero de primeira ordem, tomamos o elemento a 1 1 = 1 da matriz A . Franjando-o menor de segunda ordem 
não é igual a zero. Este menor faz fronteira com um menor de terceira ordem 
. Como não é igual a zero e não há limite menor para ele, o posto da matriz A é igual a três.
Responda:
Classificação(A) = 3 .
Considere outra maneira de encontrar o posto de uma matriz.
As seguintes transformações de matrizes são chamadas elementares:
A matriz B é chamada de equivalente à matriz A, se B é obtido de A com a ajuda de um número finito de transformações elementares. A equivalência de matrizes é denotada pelo símbolo "~", ou seja, escreve-se A ~ B.
Encontrar o posto de uma matriz usando transformações elementares de matriz é baseado na afirmação: se a matriz B é obtida da matriz A usando um número finito de transformações elementares, então Posto(A) = Posto(B).
A validade desta afirmação decorre das propriedades do determinante da matriz:
A essência do método das transformações elementaresé trazer a matriz, cujo posto precisamos encontrar, para um trapézio (em um caso particular, para um triangular superior) usando transformações elementares.
Para que serve? O posto de matrizes deste tipo é muito fácil de encontrar. É igual ao número de linhas contendo pelo menos um elemento não nulo. E como o posto da matriz não muda durante as transformações elementares, o valor resultante será o posto da matriz original.
Damos ilustrações de matrizes, uma das quais deve ser obtida após transformações. Sua forma depende da ordem da matriz.
Estas ilustrações são moldes para os quais vamos transformar a matriz A.
vamos descrever algoritmo de método.
Suponha que precisamos encontrar o posto de uma matriz não nula A de ordem (p pode ser igual a n).
Então, . Vamos multiplicar todos os elementos da primeira linha da matriz A por . Neste caso, obtemos uma matriz equivalente, denote-a A(1): 
Aos elementos da segunda linha da matriz resultante A (1), somamos os elementos correspondentes da primeira linha, multiplicados por . Aos elementos da terceira linha, adicione os elementos correspondentes da primeira linha, multiplicados por . E assim por diante até a p-ésima linha. Obtemos uma matriz equivalente, denota-a A (2): 
Se todos os elementos da matriz resultante em linhas do segundo ao p-ésimo forem iguais a zero, o posto dessa matriz é igual a um e, consequentemente, o posto da matriz original é igual a um .
Se houver pelo menos um elemento diferente de zero nas linhas do segundo ao p-ésimo, continuamos a realizar as transformações. Além disso, agimos exatamente da mesma forma, mas apenas com a parte da matriz A marcada na figura (2) 
Se , então reorganizamos as linhas e (ou) colunas da matriz A (2) de modo que o "novo" elemento se torne diferente de zero.
Seja A uma matriz de dimensões m\vezes n , e k um número natural que não exceda m e n : k\leqslant\min\(m;n\). Ordem k-ésima menor a matriz A é o determinante da matriz de ordem k formada pelos elementos na interseção de k linhas e k colunas escolhidas arbitrariamente da matriz A . Denotando menores, os números das linhas selecionadas serão indicados por índices superiores, e os números das colunas selecionadas por índices inferiores, ordenando-os em ordem crescente.
Exemplo 3.4. Escreva menores de diferentes ordens de matriz
A=\begin(pmatrix)1&2&1&0\\ 0&2&2&3\\ 1&4&3&3\end(pmatrix)\!.
Solução. A matriz A tem dimensões 3\times4 . Tem: 12 menores de 1ª ordem, por exemplo, menor M_(()_2)^(()_3)=\det(a_(32))=4; 18 menores de 2ª ordem, por exemplo, M_(()_(23))^(()^(12))=\begin(vmatriz)2&1\\2&2\end(vmatriz)=2; 4 menores de 3ª ordem, por exemplo,
M_(()_(134))^(()^(123))= \begin(vmatrix)1&1&0\\0&2&3\\ 1&3&3 \end(vmatrix)=0.
Em uma matriz A m\vezes n, o menor de ordem r é chamado básico, se for diferente de zero, e todos os menores (r + 1)-ro de ordem forem iguais a zero ou não existirem.
Classificação da matrizé chamado de ordem da base menor. Não há menor base na matriz nula. Portanto, o posto de uma matriz zero, por definição, é assumido como zero. O posto de uma matriz A é denotado \operatorname(rg)A.
Exemplo 3.5. Encontre todos os menores de base e posto de uma matriz
A=\begin(pmatriz)1&2&2&0\\0&2&2&3\\0&0&0&0\end(pmatriz)\!.
Solução. Todos os menores de terceira ordem dessa matriz são iguais a zero, pois a terceira linha desses determinantes é zero. Portanto, apenas um menor de segunda ordem localizado nas duas primeiras linhas da matriz pode ser básico. Passando por 6 menores possíveis, selecionamos diferente de zero
M_(()_(12))^(()^(12))= M_(()_(13))^(()^(12))= \begin(vmatrix)1&2\\0&2 \end( vmatrix)\!,\quad M_(()_(24))^(()^(12))= M_(()_(34))^(()^(12))= \begin(vmatrix) 2&0\\2&3\end(vmatriz)\!,\quad M_(()_(14))^(()^(12))= \begin(vmatriz)1&0\\0&3\end(vmatriz)\!.
Cada um desses cinco menores é básico. Portanto, o posto da matriz é 2.
Observações 3.2
1. Se na matriz todos os menores de ordem k são iguais a zero, então os menores de ordem superior também são iguais a zero. De fato, expandindo o (k + 1)-ro menor de ordem sobre qualquer linha, obtemos a soma dos produtos dos elementos dessa linha por k-ésima ordem menores, e eles são iguais a zero.
2. O posto de uma matriz é igual à maior ordem do menor não nulo desta matriz.
3. Se matriz quadradaé não degenerado, então sua classificação é igual à sua ordem. Se uma matriz quadrada é degenerada, então sua classificação é menor que sua ordem.
4. As designações também são usadas para classificação \operatorname(Rg)A,~ \operatorname(rank)A,~ \operatorname(rank)A.
5. Classificação da matriz do blocoé definido como a classificação de uma matriz (numérica) comum, ou seja, independentemente da sua estrutura de blocos. Nesse caso, a classificação da matriz de blocos não é menor que a classificação de seus blocos: \operatorname(rg)(A\mid B)\geqslant\operatorname(rg)A e \operatorname(rg)(A\mid B)\geqslant\operatorname(rg)B, já que todos os menores da matriz A (ou B ) também são menores da matriz de blocos (A\mid B) .
Vamos considerar os principais teoremas que expressam as propriedades de dependência linear e independência linear de colunas (linhas) de uma matriz.
Teorema 3.1 sobre o menor básico. Em uma matriz arbitrária A, cada coluna (linha) é uma combinação linear de colunas (linhas) na qual a base menor está localizada.
De fato, sem perda de generalidade, assumimos que na matriz A m\times n, a base menor está localizada nas primeiras r linhas e nas primeiras r colunas. Considere o determinante
D=\begin(vmatrix)~ a_(11)&\cdots&a_(1r)\!\!&\vline\!\!&a_(1k)~\\ ~\vdots&\ddots &\vdots\!\!&\ vline\!\!&\vdots~\\ ~a_(r1)&\cdots&a_(rr)\!\!&\vline\!\!&a_(rk)~\\\hline ~a_(s1)&\cdots&a_ (sr)\!\!&\vline\!\!&a_(sk)~\end(vmatrix),
que é obtido atribuindo os elementos correspondentes à base menor da matriz A ª linha e k-ésima coluna. Note que para qualquer 1\leqslant s\leqslant m e esse determinante é zero. Se s\leqslant r ou k\leqslant r , então o determinante D contém duas linhas idênticas ou duas colunas idênticas. Se s>r e k>r , então o determinante D é igual a zero, pois é um menor da ordem (r+l)-ro. Expandindo o determinante na última linha, obtemos
a_(s1)\cdot D_(r+11)+\ldots+ a_(sr)\cdot D_(r+1r)+a_(sk)\cdot D_(r+1\,r+1)=0,
onde D_(r+1\,j) são os complementos algébricos dos elementos da última linha. Observe que D_(r+1\,r+1)\ne0 , pois este é um menor básico. É por isso
a_(sk)=\lambda_1\cdot a_(s1)+\ldots+\lambda_r\cdot a_(sr), Onde \lambda_j=-\frac(D_(r+1\,j))(D_(r+1\,r+1)),~j=1,2,\ldots,r.
\begin(pmatrix)a_(1k)\\\vdots\\a_(mk)\end(pmatrix)= \lambda_1\cdot\! \begin(pmatrix)a_(11)\\\vdots\\a_(m1)\end(pmatrix)+\ldots \lambda_r\cdot\! \begin(pmatrix)a_(1r)\\\vdots\\a_(mr)\end(pmatrix)\!.
Essa. k -ésima coluna (para qualquer 1\leqslant k\leqslant n) é uma combinação linear das colunas do menor básico, que estava para ser provado.
O teorema básico menor serve para provar os seguintes teoremas importantes.
Teorema 3.2 (condição necessária e suficiente para que o determinante seja igual a zero). Para que um determinante seja igual a zero, é necessário e suficiente que uma de suas colunas (uma de suas linhas) seja uma combinação linear das demais colunas (linhas).
De fato, a necessidade decorre do teorema básico do menor. Se o determinante de uma matriz quadrada de enésima ordem for igual a zero, então seu posto é menor que n, ou seja, pelo menos uma coluna não está incluída na base menor. Então esta coluna escolhida, pelo Teorema 3.1, é uma combinação linear das colunas contendo o menor de base. Acrescentando, se necessário, a esta combinação outras colunas com coeficientes nulos, obtemos que a coluna selecionada é uma combinação linear das restantes colunas da matriz. A suficiência decorre das propriedades do determinante. Se, por exemplo, a última coluna A_n do determinante \det(A_1~A_2~\cdots~A_n) expressa linearmente em termos do resto
A_n=\lambda_1\cdot A_1+\lambda_2\cdot A_2+\ldots+\lambda_(n-1)\cdot A_(n-1),
em seguida, adicionando a A_n a coluna A_1 multiplicada por (-\lambda_1) , depois a coluna A_2 multiplicada por (-\lambda_2) , e assim por diante. coluna A_(n-1) multiplicada por (-\lambda_(n-1)) , obtemos o determinante \det(A_1~\cdots~A_(n-1)~o) com uma coluna zero igual a zero (propriedade 2 do determinante).
Teorema 3.3 (sobre invariância de posto sob transformações elementares). Sob transformações elementares de colunas (linhas) de uma matriz, seu posto não muda.
De fato, vamos. Suponha que, como resultado de uma transformação elementar das colunas da matriz A, obtivemos a matriz A ". Se uma transformação do tipo I foi realizada (permutação de duas colunas), então qualquer menor (r + l)-ro do ordem da matriz A" ou igual ao correspondente menor (r + l )-ro da ordem da matriz A , ou difere dela em sinal (propriedade 3 do determinante). Se uma transformação do tipo II foi realizada (multiplicação de colunas pelo número \lambda\ne0 ), então qualquer menor (r+l)-ro da ordem da matriz A" é igual ao menor correspondente (r+l)- ro da ordem da matriz A , ou difere dela fator \lambda\ne0 (propriedade 6 do determinante). Tipo III(adicionando a uma coluna de outra coluna multiplicada pelo número \Lambda ), então qualquer menor da (r + 1)ª ordem da matriz A" é igual ao menor correspondente da (r + 1)ª ordem de a matriz A (propriedade 9 do determinante), ou é igual a soma dois menores (r+l)-ro da ordem da matriz A (propriedade 8 do determinante). Portanto, sob uma transformação elementar de qualquer tipo, todos os menores (r + l) - ro da ordem da matriz A" são iguais a zero, pois todos os menores (r + l) - ro da ordem da matriz A são igual a zero. Assim, está provado que sob transformações elementares de colunas, as matrizes de posto não podem aumentar. Como as transformações inversas para elementares são elementares, o posto de uma matriz não pode diminuir sob transformações elementares de colunas, ou seja, não muda. é provado de forma semelhante que o posto de uma matriz não muda sob transformações elementares de linhas.
Consequência 1. Se uma linha (coluna) de uma matriz é uma combinação linear de suas outras linhas (colunas), essa linha (coluna) pode ser excluída da matriz sem alterar sua classificação.
De fato, tal string pode se tornar nula usando transformações elementares, e a string nula não pode ser incluída no menor básico.
Consequência 2. Se a matriz for reduzida à sua forma mais simples (1.7), então
\operatorname(rg)A=\operatorname(rg)\Lambda=r\,.
Com efeito, a matriz da forma mais simples (1.7) tem uma base menor de enésima ordem.
Consequência 3. Qualquer matriz quadrada não singular é elementar, ou seja, qualquer matriz quadrada não singular é equivalente à matriz identidade de mesma ordem.
De fato, se A é uma matriz quadrada não singular de ordem n, então \operatorname(rg)A=n(ver ponto 3 da observação 3.2). Portanto, reduzindo a matriz A à forma mais simples (1.7) por transformações elementares, obtemos a matriz identidade \Lambda=E_n , pois \operatorname(rg)A=\operatorname(rg)\Lambda=n(ver Corolário 2). Portanto, a matriz A é equivalente à matriz identidade E_n e pode ser obtida a partir dela como resultado de um número finito de transformações elementares. Isso significa que a matriz A é elementar.
Teorema 3.4 (sobre o posto de uma matriz). O posto de uma matriz é igual ao número máximo de linhas linearmente independentes dessa matriz.
De fato, deixe \operatorname(rg)A=r. Então a matriz A tem r linhas linearmente independentes. Estas são as linhas em que o menor básico está localizado. Se fossem linearmente dependentes, então este menor seria igual a zero pelo Teorema 3.2, e o posto da matriz A não seria igual a r . Vamos mostrar que r é o número máximo de linhas linearmente independentes, ou seja, quaisquer p linhas são linearmente dependentes para p>r . De fato, formamos uma matriz B a partir dessas p linhas. Como a matriz B é parte da matriz A , então \operatorname(rg)B\leqslant \operatorname(rg)A=r Isso significa que pelo menos uma linha da matriz B não está incluída na base menor dessa matriz. Então, pelo teorema da base menor, é igual a uma combinação linear de linhas na qual a base menor está localizada. Portanto, as linhas da matriz B são linearmente dependentes. Assim, a matriz A tem no máximo r linhas linearmente independentes. Consequência 1. O número máximo de linhas linearmente independentes em uma matriz é igual ao número máximo de colunas linearmente independentes: \operatorname(rg)A=\operatorname(rg)A^T. Esta afirmação decorre do Teorema 3.4 se for aplicada às linhas da matriz transposta e for levado em conta que os menores não mudam na transposição (propriedade 1 do determinante). Consequência 2. Sob transformações elementares das linhas de uma matriz, a dependência linear (ou independência linear) de qualquer sistema de colunas dessa matriz é preservada. De fato, escolhemos quaisquer k colunas da matriz A dada e formamos a matriz B a partir delas. Deixe, como resultado de transformações elementares das linhas da matriz A, a matriz A" foi obtida, e como resultado das mesmas transformações das linhas da matriz B, a matriz B" foi obtida. Pelo Teorema 3.3 \operatorname(rg)B"=\operatorname(rg)B. Portanto, se as colunas da matriz B fossem linearmente independentes, ou seja, k=\operatorname(rg)B(ver Corolário 1), então as colunas da matriz B" também são linearmente independentes, pois k=\operatorname(rg)B". Se as colunas da matriz B fossem linearmente dependentes (k>\operatorname(rg)B), então as colunas da matriz B" também são linearmente dependentes (k>\operatorname(rg)B"). Portanto, para quaisquer colunas da matriz A, a dependência linear ou independência linear é preservada sob transformações elementares de linhas. Observações 3.3 1. Em virtude do Corolário 1 do Teorema 3.4, a propriedade coluna indicada no Corolário 2 também é válida para qualquer sistema de linhas de matrizes se forem realizadas transformações elementares apenas em suas colunas. 2. O Corolário 3 do Teorema 3.3 pode ser refinado da seguinte forma: qualquer matriz quadrada não singular, usando transformações elementares apenas de suas linhas (ou apenas de suas colunas), pode ser reduzida a uma matriz identidade da mesma ordem. De fato, usando apenas transformações elementares de linhas, qualquer matriz A pode ser reduzida à forma simplificada \Lambda (Fig. 1.5) (ver Teorema 1.1). Como a matriz A é não singular (\det(A)\ne0) , suas colunas são linearmente independentes. Logo, as colunas da matriz \Lambda também são linearmente independentes (Corolário 2 do Teorema 3.4). Portanto, a forma simplificada \Lambda da matriz não singular A coincide com sua forma mais simples (Fig. 1.6) e é a matriz identidade \Lambda=E (ver Corolário 3 do Teorema 3.3). Assim, ao transformar apenas as linhas de uma matriz não singular, ela pode ser reduzida à identidade. Raciocínio semelhante também é válido para transformações elementares das colunas de uma matriz não singular. Teorema 3.5 (sobre o posto do produto de matrizes).Posição do produto e soma das matrizes
\operatorname(rg)(A\cdot B)\leqslant \min\(\operatorname(rg)A,\operatorname(rg)B\).
De fato, deixe as matrizes A e B terem tamanhos m\times p e p\times n . Atribuímos à matriz A a matriz C=AB\dois pontos\,(A\meio C). Escusado será dizer que \operatorname(rg)C\leqslant\operatorname(rg)(A\mid C), pois C é uma parte da matriz (A\mid C) (ver item 5 da Observação 3.2). Observe que cada coluna de C_j , de acordo com a operação de multiplicação de matrizes, é uma combinação linear das colunas A_1,A_2,\ldots,A_p matrizes A=(A_1~\cdots~A_p):
C_(j)=A_1\cdot b_(1j)+A_2\cdot b_(2j)+\ldots+A_(p)\cdot b_pj),\quad j=1,2,\ldots,n.
Tal coluna pode ser deletada da matriz (A\mid C) sem alterar seu posto (Corolário 1 do Teorema 3.3). Riscando todas as colunas da matriz C, obtemos: \operatorname(rg)(A\mid C)=\operatorname(rg)A. Daqui, \operatorname(rg)C\leqslant\operatorname(rg)(A\mid C)=\operatorname(rg)A. Da mesma forma, pode-se provar que a condição \operatorname(rg)C\leqslant\operatorname(rg)B, e tire uma conclusão sobre a validade do teorema.
Consequência. Se um A é uma matriz quadrada não degenerada, então \operatorname(rg)(AB)= \operatorname(rg)B e \operatorname(rg)(CA)=\operatorname(rg)C, ou seja o posto de uma matriz não muda quando ela é multiplicada à esquerda ou à direita por uma matriz quadrada não singular.
Teorema 3.6 sobre o posto da soma de matrizes. O posto da soma das matrizes não excede a soma dos postos dos termos:
\operatorname(rg)(A+B)\leqslant \operatorname(rg)A+\operatorname(rg)B.
De fato, vamos criar uma matriz (A+B\meio A\meio B). Observe que cada coluna da matriz A+B é uma combinação linear das colunas das matrizes A e B . É por isso \operatorname(rg)(A+B\mid A\mid B)= \operatorname(rg)(A\mid B). Considerando que o número de colunas linearmente independentes na matriz (A\mid B) não excede \operatorname(rg)A+\operatorname(rg)B, uma \operatorname(rg)(A+B)\leqslant \operatorname(rg)(A+B\mid A\mid B)(ver item 5 das Observações 3.2), obtemos a desigualdade requerida.
E considere também uma importante aplicação prática do tema: estudo do sistema equações lineares para compatibilidade.
A epígrafe humorística do artigo contém muita verdade. A própria palavra "classificação" geralmente está associada a algum tipo de hierarquia, na maioria das vezes com a escada da carreira. Quanto mais conhecimento, experiência, habilidades, conexões, etc., uma pessoa tem. - quanto maior for a sua posição e gama de oportunidades. Em termos juvenis, a classificação refere-se ao grau geral de "resistência".
E nossos irmãos matemáticos vivem pelos mesmos princípios. Vamos dar um passeio arbitrário matrizes zero:
Vamos pensar se na matriz apenas zeros, então de que classificação podemos falar? Todos estão familiarizados com a expressão informal "zero total". Na sociedade matrix, tudo é exatamente igual:
Classificação da matriz zeroqualquer tamanho é zero.
Observação : a matriz zero é denotada pela letra grega "theta"
A fim de entender melhor o posto da matriz, a seguir vou me basear nos materiais geometria analítica. Considere zero vetor nosso espaço tridimensional, que não define uma direção específica e é inútil para construir base afim. Do ponto de vista algébrico, as coordenadas de um dado vetor são escritas em matriz"um por três" e lógico (no sentido geométrico especificado) suponha que o posto desta matriz seja zero.
Agora vamos ver alguns diferente de zero vetores coluna e vetores linha:
Cada instância tem pelo menos um elemento não nulo, e isso é alguma coisa!
A classificação de qualquer vetor linha diferente de zero (vetor coluna) é igual a um
E de um modo geral - se na matriz tamanhos arbitrários tem pelo menos um elemento diferente de zero, então sua classificação não menos unidades.
Os vetores algébricos de linha e coluna são abstratos até certo ponto, então vamos voltar à associação geométrica. diferente de zero vetor define uma direção bem definida no espaço e é adequado para a construção base, portanto, o posto da matriz será considerado igual a um.
Bases teóricas : em álgebra linear, um vetor é um elemento de um espaço vetorial (definido por 8 axiomas), que, em particular, pode ser uma linha ordenada (ou coluna) de números reais com as operações de adição e multiplicação definidas para eles por número real. Com mais informação detalhada sobre vetores pode ser encontrado no artigo transformações lineares.
linearmente dependente(expressos um através do outro). Do ponto de vista geométrico, a segunda linha contém as coordenadas do vetor colinear 
, que não avançou a matéria na construção base tridimensional, sendo redundante nesse sentido. Assim, o posto desta matriz também é igual a um.
Reescrevemos as coordenadas dos vetores em colunas ( transpor a matriz):
O que mudou em termos de classificação? Nada. As colunas são proporcionais, o que significa que a classificação é igual a um. A propósito, observe que todas as três linhas também são proporcionais. Eles podem ser identificados com as coordenadas três vetores colineares do plano, dos quais apenas umútil para construir uma base "plana". E isso está de acordo com nosso senso geométrico de classificação.
Uma declaração importante segue do exemplo acima:
Classificação da matriz por linhas igual a classificação matriz por colunas. Já comentei um pouco sobre isso na aula sobre eficácia métodos para calcular o determinante.
Observação : dependência linear de linhas leva a dependência linear de colunas (e vice-versa). Mas, para economizar tempo e por hábito, quase sempre falarei sobre a dependência linear das cordas.
Vamos continuar a treinar nosso amado animal de estimação. Adicione as coordenadas de outro vetor colinear à matriz na terceira linha 
:
Ele nos ajudou a construir uma base tridimensional? Claro que não. Todos os três vetores caminham para frente e para trás ao longo do mesmo caminho, e a classificação da matriz é uma. Você pode pegar quantos vetores colineares quiser, digamos 100, colocar suas coordenadas em uma matriz de 100 por 3, e a classificação de tal arranha-céu ainda permanecerá uma.
Vamos nos familiarizar com a matriz cujas linhas Linearmente independente. Um par de vetores não colineares é adequado para construir uma base tridimensional. A classificação desta matriz é dois.
Qual é o posto da matriz? As linhas não parecem ser proporcionais... então, em teoria, três. No entanto, o posto dessa matriz também é igual a dois. Adicionei as duas primeiras linhas e anotei o resultado na parte inferior, ou seja, expresso linearmente terceira linha através das duas primeiras. Geometricamente, as linhas da matriz correspondem às coordenadas de três vetores coplanares, e entre este triplo há um par de camaradas não colineares.
Como você pode ver dependência linear na matriz considerada não é óbvia, e hoje vamos apenas aprender como trazê-la “para a água limpa”.
Acho que muitas pessoas adivinham qual é o posto de uma matriz!
Considere uma matriz cujas linhas Linearmente independente. Formulário de vetores base afim, e a classificação desta matriz é três.
Como você sabe, qualquer quarto, quinto, décimo vetor do espaço tridimensional será expresso linearmente em termos de vetores de base. Portanto, se qualquer número de linhas for adicionado à matriz, sua classificação ainda serão três.
Raciocínio semelhante pode ser feito para as matrizes tamanhos maiores(obviamente, já sem sentido geométrico).
Definição : classificação da matriz é o número máximo de linhas linearmente independentes. Ou: o posto de uma matriz é o número máximo de colunas linearmente independentes. Sim, sempre combinam.
Uma orientação prática importante decorre do exposto acima: o posto de uma matriz não excede sua dimensão mínima. Por exemplo, na matriz 
quatro linhas e cinco colunas. A dimensão mínima é quatro, portanto, o posto desta matriz certamente não ultrapassará 4.
Notação: na teoria e na prática mundial não existe um padrão geralmente aceito para designar a classificação da matriz, o mais comum pode ser encontrado: - como dizem, um inglês escreve uma coisa, um alemão outra. Portanto, com base na conhecida anedota sobre o inferno americano e russo, vamos designar a classificação da matriz com uma palavra nativa. Por exemplo: . E se a matriz for "sem nome", da qual existem muitos, você pode simplesmente escrever .
Se nossa avó tivesse uma quinta coluna na matriz, então outra menor de 4ª ordem (“azul”, “framboesa” + 5ª coluna) deveria ter sido calculada.
Conclusão: a ordem máxima de um menor diferente de zero é três, então .
Talvez nem todos tenham compreendido totalmente essa frase: o menor de 4ª ordem é igual a zero, mas entre os menores de 3ª ordem havia um diferente de zero - portanto, a ordem máxima diferente de zero menor e igual a três.
Surge a pergunta: por que não calcular imediatamente o determinante? Bem, em primeiro lugar, na maioria das tarefas, a matriz não é quadrada e, em segundo lugar, mesmo que você obtenha um valor diferente de zero, a tarefa será rejeitada com alta probabilidade, pois geralmente implica um padrão "de baixo para cima" solução. E no exemplo considerado, o determinante nulo de 4ª ordem ainda nos permite afirmar que o posto da matriz é apenas inferior a quatro.
Devo admitir que eu mesmo criei o problema analisado para explicar melhor o método de fazer fronteira com menores. Na prática, tudo é mais simples:
Exemplo 2
Encontre o posto de uma matriz pelo método de franjas menores 
Solução e resposta no final da lição.
Quando o algoritmo está rodando mais rápido? Vamos voltar para a mesma matriz quatro por quatro 
. Obviamente, a solução será a mais curta no caso de "bom" menores de canto: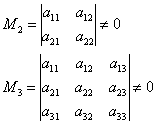
E, se , então , caso contrário - .
Pensar não é nada hipotético - há muitos exemplos em que tudo se limita apenas a menores angulares.
No entanto, em alguns casos, outro método é mais eficaz e preferível:
Esta seção destina-se a leitores que já estão familiarizados com método Gauss e pouco a pouco colocaram as mãos nele.
Do ponto de vista técnico, o método não é novo:
1) usando transformações elementares, trazemos a matriz para uma forma escalonada;
2) o posto da matriz é igual ao número de linhas.
É bem claro que usar o método de Gauss não altera a classificação da matriz, e a essência aqui é extremamente simples: de acordo com o algoritmo, no decorrer das transformações elementares, todas as linhas proporcionais desnecessárias (linearmente dependentes) são identificadas e removidas, resultando em um “resíduo seco” - o número máximo de retas linearmente independentes.
Vamos transformar a velha matriz familiar com as coordenadas de três vetores colineares: 
(1) A primeira linha foi adicionada à segunda linha, multiplicada por -2. A primeira linha foi adicionada à terceira linha.
(2) As linhas zero são excluídas.
Portanto, resta uma linha, portanto . Desnecessário dizer que isso é muito mais rápido do que calcular nove zeros menores de 2ª ordem e só então tirar uma conclusão.
Eu te lembro que em si matriz algébrica nada pode ser alterado e as transformações são realizadas apenas com o objetivo de descobrir a classificação! A propósito, vamos nos deter na questão novamente, por que não? Matriz de origem 
carrega informações que são fundamentalmente diferentes das informações de matriz e linha. Em alguns modelos matemáticos(sem exagero) a diferença de um número pode ser uma questão de vida ou morte. ... Lembrei-me dos professores de matemática das classes primária e secundária, que cortavam impiedosamente a nota em 1-2 pontos pela menor imprecisão ou desvio do algoritmo. E foi terrivelmente decepcionante quando, em vez dos "cinco" aparentemente garantidos, acabou "bom" ou ainda pior. O entendimento veio muito mais tarde - de que outra forma confiar a uma pessoa satélites, ogivas nucleares e usinas de energia? Mas não se preocupe, não trabalho nessas áreas =)
Vamos passar para tarefas mais significativas, onde, entre outras coisas, vamos nos familiarizar com importantes técnicas computacionais método Gauss:
Exemplo 3
Encontre o posto de uma matriz usando transformações elementares 
Solução: dada uma matriz de quatro por cinco, o que significa que sua classificação certamente não é maior que 4.
Na primeira coluna, não há 1 ou -1, portanto, etapas adicionais são necessárias para obter pelo menos uma unidade. Ao longo de toda a existência do site, repetidamente me perguntam: “É possível reorganizar as colunas durante as transformações elementares?”. Aqui - reorganizei a primeira ou a segunda coluna e está tudo bem! Na maioria das tarefas onde método Gauss, as colunas podem realmente ser reorganizadas. MAS NÃO. E a questão nem é uma possível confusão com variáveis, a questão é que no curso clássico matemática superior essa ação tradicionalmente não é considerada, portanto, tal reverência será vista de forma MUITO torta (ou até forçada a refazer tudo).
O segundo ponto diz respeito aos números. No decurso da decisão, é útil orientar-se pela seguinte regra prática: transformações elementares devem, se possível, reduzir os números da matriz. Com efeito, é muito mais fácil trabalhar com um-dois-três do que, por exemplo, com 23, 45 e 97. E a primeira ação visa não só obter uma unidade na primeira coluna, mas também eliminar os números 7 e 11.
Primeiro a solução completa, depois os comentários: 
(1) A primeira linha foi adicionada à segunda linha, multiplicada por -2. A primeira linha foi adicionada à terceira linha, multiplicada por -3. E para a pilha: a 1ª linha, multiplicada por -1, foi adicionada à 4ª linha.
(2) As últimas três linhas são proporcionais. Excluídas a 3ª e 4ª linhas, a segunda linha foi movida para o primeiro lugar.
(3) A primeira linha foi adicionada à segunda linha, multiplicada por -3.
A matriz reduzida a uma forma escalonada tem duas linhas.
Responda:
Agora é sua vez de torturar a matriz quatro por quatro:
Exemplo 4
Encontre o posto de uma matriz usando o método gaussiano 
eu te lembro que método Gauss não implica rigidez inequívoca, e sua solução provavelmente será diferente da minha solução. Uma breve amostra da tarefa no final da lição.
Na prática, muitas vezes não é dito qual método deve ser usado para encontrar a classificação. Em tal situação, deve-se analisar a condição - para algumas matrizes é mais racional realizar a solução por meio de menores, enquanto para outras é muito mais lucrativo aplicar transformações elementares:
Exemplo 5
Encontrar o posto de uma matriz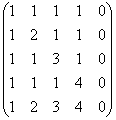 
Solução: a primeira maneira de alguma forma desaparece imediatamente =)
Um pouco mais alto, aconselhei não mexer nas colunas da matriz, mas quando houver coluna zero, ou colunas proporcionais / correspondentes, ainda vale a pena amputar: 
(1) A quinta coluna é zero, nós a removemos da matriz. Assim, o posto da matriz é no máximo quatro. A primeira linha é multiplicada por -1. Esse é outro recurso característico do método gaussiano, que torna a seguinte ação um passeio agradável:
(2) A todas as linhas, começando pela segunda, foi acrescentada a primeira linha.
(3) A primeira linha foi multiplicada por -1, a terceira linha foi dividida por 2, a quarta linha foi dividida por 3. A segunda linha multiplicada por -1 foi adicionada à quinta linha.
(4) A terceira linha foi adicionada à quinta linha, multiplicada por -2.
(5) As duas últimas linhas são proporcionais, excluímos a quinta.
O resultado são 4 linhas.
Responda:
Edifício padrão de cinco andares para auto-exploração:
Exemplo 6
Encontrar o posto de uma matriz
Solução curta e resposta no final da lição.
Deve-se notar que a frase "classificação da matriz" não é tão comum na prática e, na maioria dos problemas, você pode passar sem ela. Mas há uma tarefa em que o conceito em consideração é o principal. ator, e no final do artigo veremos esta aplicação prática:
Muitas vezes, além de resolver sistemas de equações lineares de acordo com a condição, é necessário primeiro examiná-la quanto à compatibilidade, ou seja, provar que existe alguma solução. Um papel fundamental nesta verificação é desempenhado por teorema de Kronecker-Capelli, que formularei na forma necessária:
Se classificar matrizes do sistema igual a classificação sistema de matriz aumentada, então o sistema é compatível e, se esse número coincidir com o número de incógnitas, então solução é única.
Assim, para estudar a compatibilidade do sistema, é necessário verificar a igualdade 
, Onde - matriz do sistema(lembre-se da terminologia da lição método Gauss), uma - sistema de matriz aumentada(ou seja, matriz com coeficientes em variáveis + coluna de termos livres).
Para calcular o posto de uma matriz, pode-se aplicar o método dos menores limítrofes ou o método de Gauss. Considere o método de Gauss ou o método das transformações elementares.
O posto de uma matriz é a ordem máxima de seus menores, dentre os quais haja pelo menos um que não seja igual a zero.
O posto de um sistema de linhas (colunas) é o número máximo de linhas (colunas) linearmente independentes desse sistema.
O algoritmo para encontrar o posto de uma matriz pelo método de franjas menores:
Vamos analisar o algoritmo com mais detalhes. Primeiro, considere os menores de primeira ordem (elementos da matriz) da matriz UMA. Se todos forem zero, então postoA = 0. Se houver menores de primeira ordem (elementos da matriz) que não sejam iguais a zero M1 ≠ 0, então a classificação rangA ≥ 1.
M1. Se houver tais menores, então serão menores de segunda ordem. Se todos os menores fazem fronteira com o menor M1 são iguais a zero, então posto A = 1. Se houver pelo menos um menor de segunda ordem que não seja igual a zero M2 ≠ 0, então a classificação rangA ≥ 2.
Verifique se há menores limítrofes para o menor M2. Se houver tais menores, então serão menores de terceira ordem. Se todos os menores fazem fronteira com o menor M2 são iguais a zero, então posto A = 2. Se houver pelo menos um menor de terceira ordem que não seja igual a zero M3 ≠ 0, então a classificação rangA ≥ 3.
Verifique se há menores limítrofes para o menor M3. Se houver tais menores, serão menores de quarta ordem. Se todos os menores fazem fronteira com o menor M3 são iguais a zero, então classificação A = 3. Se houver pelo menos um menor de quarta ordem que não seja igual a zero M4 ≠ 0, então a classificação rangA ≥ 4.
Verificando se há um menor limítrofe para um menor M4, e assim por diante. O algoritmo para se em algum estágio os menores limítrofes forem iguais a zero ou o menor limítrofe não puder ser obtido (não há linhas ou colunas na matriz). A ordem de um menor diferente de zero, que conseguimos compor, será a classificação da matriz.
Considerar este método Por exemplo. Dada uma matriz 4x5:
Esta matriz não pode ter um posto maior que 4. Além disso, esta matriz possui elementos diferentes de zero (um menor de primeira ordem), o que significa que o posto da matriz é ≥ 1.
vamos fazer um menor 2º ordem. Vamos começar do canto.
Como o determinante é igual a zero, compomos outro menor.
Encontre o determinante desse menor.
Determine que o menor dado é -2 . Então o posto da matriz ≥ 2 .
Se esse menor fosse igual a 0, outros menores seriam adicionados. Até ao final, todos os menores teriam sido sorteados nas filas 1 e 2. Depois nas linhas 1 e 3, nas linhas 2 e 3, nas linhas 2 e 4, até encontrarem um menor diferente de 0, por exemplo:
Se todos os menores de segunda ordem forem 0, então o posto da matriz será 1. A solução pode ser interrompida.
3º ordem.
O menor acabou não sendo zero. significa o posto da matriz ≥ 3 .
Se este menor fosse zero, então outros menores teriam que ser compostos. Por exemplo:
Se todos os menores de terceira ordem forem 0, o posto da matriz será 2. A solução pode ser interrompida.
Continuamos procurando o posto de uma matriz. vamos fazer um menor 4º ordem.
Vamos encontrar o determinante deste menor.
O determinante do menor acabou por ser igual 0 . Vamos construir outro menor.
Vamos encontrar o determinante deste menor.
O menor acabou por ser igual 0 .
Construir um menor 5 ª ordem não funcionará, não há linha nesta matriz para isso. O último menor diferente de zero foi 3º ordem, então o posto da matriz é 3 .
Elementar As seguintes transformações de matrizes são chamadas:
1) permutação de quaisquer duas linhas (ou colunas),
2) multiplicar uma linha (ou coluna) por um número diferente de zero,
3) adicionar a uma linha (ou coluna) outra linha (ou coluna) multiplicada por algum número.
As duas matrizes são chamadas equivalente, se um deles é obtido do outro com a ajuda de um conjunto finito de transformações elementares.
Matrizes equivalentes não são, de um modo geral, iguais, mas seus postos são iguais. Se as matrizes A e B são equivalentes, isso é escrito como: A ~ B.
Canônico Uma matriz é uma matriz que possui vários 1s consecutivos no início da diagonal principal (cujo número pode ser zero) e todos os outros elementos são iguais a zero, por exemplo,
Com a ajuda de transformações elementares de linhas e colunas, qualquer matriz pode ser reduzida a uma matriz canônica. Classificação da matriz canônica é igual ao número unidades em sua diagonal principal.
Exemplo 2 Encontrar o posto de uma matriz
A= 
e trazê-lo para a forma canônica.
Solução. Subtraia a primeira linha da segunda linha e reorganize essas linhas:
.
Agora, da segunda e terceira linhas, subtraia a primeira, multiplicada por 2 e 5, respectivamente:
;
subtraia a primeira da terceira linha; obtemos a matriz
B = 
,
que é equivalente à matriz A, pois dela se obtém por meio de um conjunto finito de transformações elementares. Obviamente, o posto da matriz B é 2 e, portanto, r(A)=2. A matriz B pode ser facilmente reduzida à canônica. Subtraindo a primeira coluna, multiplicada por números adequados, de todas as subseqüentes, voltamos a zero todos os elementos da primeira linha, exceto o primeiro, e os elementos das linhas restantes não mudam. Então, subtraindo a segunda coluna, multiplicada pelos números apropriados, de todas as subseqüentes, voltamos a zero todos os elementos da segunda linha, exceto a segunda, e obtemos a matriz canônica:
.
Kronecker - Teorema de Capelli- critério de compatibilidade do sistema de equações algébricas lineares:
Para que um sistema linear seja compatível, é necessário e suficiente que o posto da matriz estendida desse sistema seja igual ao posto de sua matriz principal.
Precisar
Deixar sistema articulação. Então há números são, o que . Portanto, a coluna é uma combinação linear das colunas da matriz. Do fato de que a classificação de uma matriz não mudará se o sistema de suas linhas (colunas) for excluído ou uma linha (coluna) for atribuída, que é uma combinação linear de outras linhas (colunas), segue-se que .
Adequação
Deixar . Vamos pegar alguns menores básicos na matriz. Desde , então também será a base menor da matriz . Então, de acordo com o teorema de base menor, a última coluna da matriz será uma combinação linear das colunas base, ou seja, as colunas da matriz . Portanto, a coluna de membros livres do sistema é uma combinação linear das colunas da matriz.
Consequências
Número de variáveis principais sistemas igual ao posto do sistema.
Articulação sistema será definido (sua solução é única) se o posto do sistema for igual ao número de todas as suas variáveis.
Sistema homogêneo de equações
Frase15 . 2 Sistema homogêneo de equações
|
|
é sempre colaborativo.
Prova. Para este sistema, o conjunto de números , , , é uma solução.
Nesta seção, usaremos a notação matricial do sistema: .
Frase15 . 3 A soma das soluções de um sistema homogêneo de equações lineares é uma solução desse sistema. Uma solução multiplicada por um número também é uma solução.
Prova. Sejam e sirvam como soluções do sistema. Então e. Deixar . Então
Como , então é uma solução.
Let Ser um número arbitrário, . Então
Como , então é uma solução.
Consequência15 . 1 Se um sistema homogêneo equação linear tem uma solução diferente de zero, então ela tem infinitas soluções diferentes.
De fato, multiplicando uma solução diferente de zero por números diferentes, obteremos soluções diferentes.
Definição15
.
5
Diremos que as soluções 
forma de sistemas sistema de decisão fundamental se as colunas 
formam um sistema linearmente independente e qualquer solução para o sistema é uma combinação linear dessas colunas.
