Com a matriz A, se existe um número l tal que AX = lX.
Neste caso, o número l é chamado autovalor operador (matriz A) correspondente ao vetor X.
Em outras palavras, um autovetor é um vetor que, sob a ação de um operador linear, se transforma em um vetor colinear, ou seja, basta multiplicar por algum número. Em contraste, vetores impróprios são mais difíceis de transformar.
Escrevemos a definição do autovetor como um sistema de equações:
Vamos mover todos os termos para o lado esquerdo:
O último sistema pode ser escrito na forma matricial da seguinte forma:
(A - lE)X \u003d O
O sistema resultante sempre tem uma solução zero X = O. Tais sistemas em que todos os termos livres são iguais a zero são chamados homogêneo. Se a matriz de tal sistema é quadrada e seu determinante não é igual a zero, então, pelas fórmulas de Cramer, sempre obtemos única decisão- zero. Pode-se provar que o sistema tem soluções não nulas se e somente se o determinante desta matriz for igual a zero, ou seja,
|A - lE| = 
= 0
Esta equação com incógnita l é chamada equação característica (polinômio característico) matriz A (operador linear).
Pode-se provar que o polinômio característico de um operador linear não depende da escolha da base.
Por exemplo, vamos encontrar os autovalores e autovetores do operador linear dado pela matriz A = .
Para isso, compomos a equação característica |А - lЕ| = 
\u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; autovalores l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.
Para encontrar os autovetores, resolvemos dois sistemas de equações
(A + 5E) X = O
(A - 7E) X = O
Para o primeiro deles, a matriz expandida terá a forma
,
de onde x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, ou seja X (1) \u003d (- (2/3) s; s).
Para o segundo deles, a matriz expandida terá a forma
,
de onde x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, ou seja X (2) \u003d ((2/3) s 1; s 1).
Assim, os autovetores deste operador linear são todos os vetores da forma (-(2/3)c; c) com autovalor (-5) e todos os vetores da forma ((2/3)c 1 ; c 1) com autovalor 7 .
Pode-se provar que a matriz do operador A na base composta por seus autovetores é diagonal e tem a forma:
,
onde l i são os autovalores dessa matriz.
A recíproca também é verdadeira: se a matriz A em alguma base for diagonal, então todos os vetores dessa base serão autovetores dessa matriz.
Também pode ser provado que se um operador linear tem n autovalores distintos aos pares, então os autovetores correspondentes são linearmente independentes, e a matriz deste operador na base correspondente tem uma forma diagonal.
Vamos explicar isso com o exemplo anterior. Tomemos valores arbitrários diferentes de zero c e c 1 , mas tais que os vetores X (1) e X (2) sejam linearmente independentes, ou seja, formaria uma base. Por exemplo, seja c \u003d c 1 \u003d 3, depois X (1) \u003d (-2; 3), X (2) \u003d (2; 3).
Vamos verificar a independência linear desses vetores:
12 ≠ 0. Nesta nova base, a matriz A terá a forma A * = .
Para verificar isso, usamos a fórmula A * = C -1 AC. Vamos encontrar C -1 primeiro.
C-1 = 
;
forma quadrática f (x 1, x 2, x n) de n variáveis é chamado de soma, cada termo do qual é o quadrado de uma das variáveis, ou o produto de duas variáveis diferentes, tomadas com um certo coeficiente: f (x 1 , x 2, x n) = 
(aij = aji).
A matriz A, composta por esses coeficientes, é chamada matriz forma quadrática. É sempre simétrico matriz (ou seja, uma matriz simétrica em torno da diagonal principal, a ij = a ji).
Na notação matricial, a forma quadrática tem a forma f(X) = X T AX, onde
De fato
Por exemplo, vamos escrever a forma quadrática na forma matricial.
Para fazer isso, encontramos uma matriz de forma quadrática. Seus elementos diagonais são iguais aos coeficientes nos quadrados das variáveis, e os demais elementos são iguais à metade dos coeficientes correspondentes da forma quadrática. É por isso
Seja a coluna-matriz de variáveis X obtida por uma transformação linear não degenerada da coluna-matriz Y, ou seja. X = CY, onde C é uma matriz não degenerada de ordem n. Então a forma quadrática f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.
Assim, sob uma transformação linear não degenerada C, a matriz da forma quadrática toma a forma: A * = C T AC.
Por exemplo, vamos encontrar a forma quadrática f(y 1, y 2) obtida da forma quadrática f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 por uma transformação linear.
A forma quadrática é chamada canônico(Tem visão canônica) se todos os seus coeficientes a ij = 0 para i ≠ j, ou seja.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.
Sua matriz é diagonal.
Teorema(a prova não é dada aqui). Qualquer forma quadrática pode ser reduzida a uma forma canônica usando uma transformação linear não degenerada.
Por exemplo, vamos reduzir à forma canônica a forma quadrática
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
Para fazer isso, primeiro selecione o quadrado completo para a variável x 1:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5 x 2 2 - x 2 x 3.
Agora selecionamos o quadrado completo para a variável x 2:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.
Em seguida, a transformação linear não degenerada y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 e y 3 \u003d x 3 traz essa forma quadrática para a forma canônica f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .
Observe que a forma canônica de uma forma quadrática é definida de forma ambígua (a mesma forma quadrática pode ser reduzida à forma canônica jeitos diferentes). No entanto, o jeitos diferentes formas canônicas têm um número propriedades comuns. Em particular, o número de termos com coeficientes positivos (negativos) de uma forma quadrática não depende de como a forma é reduzida a essa forma (por exemplo, no exemplo considerado sempre haverá dois coeficientes negativos e um positivo). Essa propriedade é chamada de lei da inércia das formas quadráticas.
Vamos verificar isso reduzindo a mesma forma quadrática à forma canônica de uma maneira diferente. Vamos iniciar a transformação com a variável x 2:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, onde y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 e y 3 = x 1 . Aqui, um coeficiente negativo -3 em y 1 e dois coeficientes positivos 3 e 2 em y 2 e y 3 (e usando outro método, obtivemos um coeficiente negativo (-5) em y 2 e dois coeficientes positivos: 2 em y 1 e 1/20 para y 3).
Deve-se notar também que o posto de uma matriz de forma quadrática, chamado o posto da forma quadrática, é igual ao número coeficientes diferentes de zero da forma canônica e não muda sob transformações lineares.
A forma quadrática f(X) é chamada positivamente (negativo) certo, se para todos os valores das variáveis que não são simultaneamente iguais a zero, é positivo, ou seja. f(X) > 0 (negativo, ou seja,
f(X)< 0).
Por exemplo, a forma quadrática f 1 (X) \u003d x 1 2 + x 2 2 é definida positiva, porque é a soma dos quadrados, e a forma quadrática f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 é definida negativa, porque representa pode ser representado como f 2 (X) \u003d - (x 1 - x 2) 2.
Na maioria das situações práticas, é um pouco mais difícil estabelecer a definição de sinal de uma forma quadrática, então um dos seguintes teoremas é usado para isso (nós os formulamos sem provas).
Teorema. Uma forma quadrática é positiva (negativa) definida se e somente se todos os autovalores de sua matriz são positivos (negativos).
Teorema(critério de Sylvester). Uma forma quadrática é definida positiva se e somente se todos os menores principais da matriz desta forma são positivos.
Maior (canto) menor A k-ésima ordem da matriz A de n-ésima ordem é chamada de determinante da matriz, composta pelas k primeiras linhas e colunas da matriz A().
Observe que para formas quadráticas negativas-definidas, os sinais dos menores principais se alternam e os menores de primeira ordem devem ser negativos.
Por exemplo, examinamos a forma quadrática f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 para definição de sinal.
= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17; 
. Portanto, a forma quadrática é definida positiva.
Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 = 2 > 0. O menor principal de segunda ordem D 2 = = 6 - 4 = 2 > 0. Portanto, de acordo com o critério de Sylvester, a forma quadrática é positiva definida.
Examinamos outra forma quadrática para definição de sinal, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Método 1. Vamos construir uma matriz de forma quadrática А = . A equação característica terá a forma 
= (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17; 
. Portanto, a forma quadrática é definida negativa.
Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Portanto, de acordo com o critério de Sylvester, a forma quadrática é definida negativa (os sinais dos menores principais se alternam, a partir de menos).
E como outro exemplo, examinamos a forma quadrática f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 para definição de sinal.
Método 1. Vamos construir uma matriz de forma quadrática А = . A equação característica terá a forma 
= (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41; 
.
Um desses números é negativo e o outro é positivo. Os sinais dos autovalores são diferentes. Portanto, uma forma quadrática não pode ser definida negativa ou positiva, ou seja, esta forma quadrática não é definida por sinal (pode assumir valores de qualquer sinal).
Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 = 2 > 0. O menor principal de segunda ordem D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
Um autovetor de uma matriz quadrada é aquele que, quando multiplicado por uma dada matriz, resulta em um vetor colinear. Em palavras simples, quando uma matriz é multiplicada por um autovetor, este último permanece o mesmo, mas multiplicado por algum número.
Um autovetor é um vetor diferente de zero V, que, quando multiplicado por uma matriz quadrada M, torna-se ele mesmo, aumentado por algum número λ. NO notação algébrica parece:
M × V = λ × V,
onde λ é um autovalor da matriz M.
Vamos considerar um exemplo numérico. Por conveniência de escrita, os números na matriz serão separados por um ponto e vírgula. Digamos que temos uma matriz:
Vamos multiplicar por um vetor coluna:
Ao multiplicar uma matriz por um vetor coluna, também obtemos um vetor coluna. Em linguagem matemática estrita, a fórmula para multiplicar uma matriz 2 × 2 por um vetor coluna ficaria assim:
M11 significa o elemento da matriz M, situado na primeira linha e primeira coluna, e M22 é o elemento localizado na segunda linha e segunda coluna. Para nossa matriz, esses elementos são M11 = 0, M12 = 4, M21 = 6, M22 10. Para um vetor coluna, esses valores são V11 = –2, V21 = 1. De acordo com esta fórmula, obtemos o seguinte resultado do produto de uma matriz quadrada por um vetor:
Por conveniência, escrevemos o vetor coluna em uma linha. Assim, multiplicamos a matriz quadrada pelo vetor (-2; 1), resultando no vetor (4; -2). Obviamente, este é o mesmo vetor multiplicado por λ = -2. lambda em este caso denota um autovalor da matriz.
O autovetor de uma matriz é um vetor colinear, ou seja, um objeto que não muda de posição no espaço quando é multiplicado por uma matriz. O conceito de colinearidade em álgebra vetorial é semelhante ao termo de paralelismo em geometria. Na interpretação geométrica, vetores colineares são segmentos paralelos direcionados comprimentos diferentes. Desde o tempo de Euclides, sabemos que uma única linha tem um número infinito de linhas paralelas a ela, então é lógico supor que cada matriz tem um número infinito de autovetores.
Do exemplo anterior, pode-se ver que ambos (-8; 4), e (16; -8) e (32, -16) podem ser autovetores. Todos estes são vetores colineares correspondentes ao autovalor λ = -2. Ao multiplicar a matriz original por esses vetores, ainda obteremos um vetor como resultado, que difere do original por 2 vezes. É por isso que, ao resolver problemas para encontrar um autovetor, é necessário encontrar apenas objetos vetoriais linearmente independentes. Na maioria das vezes, para uma matriz n × n, há n-ésimo número de autovetores. Nossa calculadora é projetada para a análise de matrizes quadradas de segunda ordem, então quase sempre dois autovetores serão encontrados como resultado, exceto quando eles coincidem.
No exemplo acima, sabíamos de antemão o autovetor da matriz original e determinamos visualmente o número lambda. Porém, na prática, tudo acontece ao contrário: no início há autovalores e só então os autovetores.
Vamos olhar para a matriz original M novamente e tentar encontrar ambos os seus autovetores. Então a matriz fica assim:
Para começar, precisamos determinar o autovalor λ, para o qual precisamos calcular o determinante da seguinte matriz:
Esta matriz é obtida subtraindo a incógnita λ dos elementos da diagonal principal. O determinante é determinado pela fórmula padrão:
Como nosso vetor não deve ser zero, tomamos a equação resultante como linearmente dependente e igualamos nosso determinante detA a zero.
(0 − λ) × (10 − λ) − 24 = 0
Vamos abrir os colchetes e obter a equação característica da matriz:
λ 2 − 10λ − 24 = 0
Isso é padrão Equação quadrática, que deve ser resolvido em termos do discriminante.
D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196
A raiz do discriminante é sqrt(D) = 14, então λ1 = -2, λ2 = 12. Agora, para cada valor lambda, precisamos encontrar um autovetor. Vamos expressar os coeficientes do sistema para λ = -2.
Nesta fórmula, E é matriz de identidade. Com base na matriz obtida, compomos um sistema de equações lineares:
2x + 4a = 6x + 12a
onde xey são elementos do autovetor.
Vamos coletar todos os X à esquerda e todos os Y à direita. Obviamente - 4x = 8y. Divida a expressão por - 4 e obtenha x = -2y. Agora podemos determinar o primeiro autovetor da matriz tomando quaisquer valores das incógnitas (lembre-se da infinidade de autovetores linearmente dependentes). Vamos tomar y = 1, então x = -2. Portanto, o primeiro autovetor se parece com V1 = (–2; 1). Volte ao início do artigo. Foi por esse objeto vetorial que multiplicamos a matriz para demonstrar o conceito de um autovetor.
Agora vamos encontrar o autovetor para λ = 12.
Vamos compor o mesmo sistema de equações lineares;
Agora vamos tomar x = 1, portanto y = 3. Assim, o segundo autovetor se parece com V2 = (1; 3). Ao multiplicar a matriz original por este vetor, o resultado será sempre o mesmo vetor multiplicado por 12. Isso completa o algoritmo de solução. Agora você sabe como definir manualmente um autovetor de uma matriz.
O programa opera de acordo com o algoritmo acima, minimizando o processo de solução. É importante ressaltar que no programa o lambda é denotado pela letra “c”. Vejamos um exemplo numérico.
Vamos tentar definir autovetores para a seguinte matriz:
Vamos inserir esses valores nas células da calculadora e obter a resposta da seguinte forma:
Assim, obtivemos dois autovetores linearmente independentes.
Álgebra linear e geometria analítica são assuntos padrão para qualquer calouro em engenharia. Um grande número de vetores e matrizes é assustador, e é fácil cometer um erro em cálculos tão complicados. Nosso programa permitirá que os alunos verifiquem seus cálculos ou resolvam automaticamente o problema de encontrar um autovetor. Existem outras calculadoras de álgebra linear em nosso catálogo, use-as em seu estudo ou trabalho.
Como inserir fórmulas matemáticas no site?
Se você precisar adicionar uma ou duas fórmulas matemáticas a uma página da Web, a maneira mais fácil de fazer isso é conforme descrito no artigo: as fórmulas matemáticas são facilmente inseridas no site na forma de imagens que o Wolfram Alpha gera automaticamente. Além da simplicidade, este método universal ajudará a melhorar a visibilidade do site em motores de busca. Está funcionando há muito tempo (e acho que funcionará para sempre), mas está moralmente desatualizado.
Se você está constantemente usando fórmulas matemáticas em seu site, então eu recomendo que você use MathJax, uma biblioteca JavaScript especial que exibe notação matemática em navegadores da web usando marcação MathML, LaTeX ou ASCIIMathML.
Existem duas maneiras de começar a usar o MathJax: (1) usando um código simples, você pode conectar rapidamente um script MathJax ao seu site, que será carregado automaticamente de um servidor remoto no momento certo (lista de servidores); (2) carregue o script MathJax de um servidor remoto para o seu servidor e conecte-o a todas as páginas do seu site. O segundo método é mais complexo e demorado e permitirá que você acelere o carregamento das páginas do seu site, e se o servidor MathJax pai ficar temporariamente indisponível por algum motivo, isso não afetará seu próprio site de forma alguma. Apesar dessas vantagens, optei pelo primeiro método, por ser mais simples, rápido e não exigir habilidades técnicas. Siga meu exemplo e em 5 minutos você poderá usar todos os recursos do MathJax em seu site.
Você pode conectar o script da biblioteca MathJax de um servidor remoto usando duas opções de código retiradas do site principal do MathJax ou da página de documentação:
Uma dessas opções de código precisa ser copiada e colada no código da sua página da web, de preferência entre as tags
e ou logo após a etiqueta . De acordo com a primeira opção, o MathJax carrega mais rápido e diminui a velocidade da página. Mas a segunda opção rastreia e carrega automaticamente as versões mais recentes do MathJax. Se você inserir o primeiro código, ele precisará ser atualizado periodicamente. Se você colar o segundo código, as páginas carregarão mais lentamente, mas você não precisará monitorar constantemente as atualizações do MathJax.A maneira mais fácil de conectar o MathJax é no Blogger ou WordPress: no painel de controle do site, adicione um widget projetado para inserir código JavaScript de terceiros, copie a primeira ou segunda versão do código de carregamento acima e coloque o widget mais próximo de o início do modelo (a propósito, isso não é necessário, pois o script MathJax é carregado de forma assíncrona). Isso é tudo. Agora aprenda a sintaxe de marcação MathML, LaTeX e ASCIIMathML e você estará pronto para incorporar fórmulas matemáticas em suas páginas da web.
Qualquer fractal é construído de acordo com uma determinada regra, que é aplicada consistentemente um número ilimitado de vezes. Cada um desses momentos é chamado de iteração.
O algoritmo iterativo para construir uma esponja de Menger é bastante simples: o cubo original de lado 1 é dividido por planos paralelos às suas faces em 27 cubos iguais. Um cubo central e 6 cubos adjacentes a ele ao longo das faces são removidos dele. Acontece um conjunto composto por 20 cubos menores restantes. Fazendo o mesmo com cada um desses cubos, obtemos um conjunto composto por 400 cubos menores. Continuando esse processo indefinidamente, obtemos a esponja Menger.
Definição 9.3. Vetor X chamado próprio vetor matrizes MAS se existe esse número λ, que a igualdade vale: MAS X= λ X, ou seja, o resultado da aplicação a X transformação linear dada pela matriz MAS, é a multiplicação desse vetor pelo número λ . O próprio número λ chamado próprio número matrizes MAS.
Substituindo em fórmulas (9.3) x`j = λxj, obtemos um sistema de equações para determinar as coordenadas do autovetor:
. (9.5)
Este linear sistema homogêneo terá uma solução não trivial somente se seu determinante principal for 0 (regra de Cramer). Escrevendo esta condição no formulário:
obtemos uma equação para determinar os autovalores λ chamado equação característica. Resumidamente, pode ser representado da seguinte forma:
| A-λE | = 0, (9.6)
já que seu lado esquerdo é o determinante da matriz A-λE. Polinômio em relação a λ | A-λE| chamado polinômio característico matrizes A.
Propriedades do polinômio característico:
1) O polinômio característico de uma transformação linear não depende da escolha da base. Prova. 
(ver (9.4)), mas 
Consequentemente, . Assim, não depende da escolha da base. Portanto, e | A-λE| não muda na transição para uma nova base.
2) Se a matriz MAS transformação linear é simétrico(Essa. um ij = um ji), então todas as raízes da equação característica (9.6) são números reais.
Propriedades de autovalores e autovetores:
1) Se escolhermos uma base de autovetores x 1, x 2, x 3 correspondente aos autovalores λ 1 , λ 2 , λ 3 matrizes MAS, então nesta base a transformação linear A tem uma matriz diagonal:
(9.7) A prova desta propriedade segue da definição de autovetores.
2) Se a transformação autovalores MAS são diferentes, então os autovetores correspondentes a eles são linearmente independentes.
3) Se o polinômio característico da matriz MAS tem três raízes diferentes, então em alguma base a matriz MAS tem uma forma diagonal.
Vamos encontrar os autovalores e autovetores da matriz Vamos fazer a equação característica: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7 λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
Encontre as coordenadas dos autovetores correspondentes a cada valor encontrado λ. De (9.5) segue que se X (1) ={x 1 , x 2 , x 3) é o autovetor correspondente a λ 1 = -2, então
- conjunta, mas sistema indefinido. Sua solução pode ser escrita como X (1)
={uma,0,-uma), onde a é qualquer número. Em particular, se você precisar que | x (1)
|=1, X (1)
=
Substituindo no sistema (9.5) λ 2 = 3, obtemos um sistema para determinar as coordenadas do segundo autovetor - x (2) ={y1, y2, y3}:
, Onde X (2)
={b,-b,b) ou, desde | x (2)
|=1, x (2)
= 
Por λ 3 = 6 encontre o autovetor x (3) ={z1, z2, z3}:
, x (3)
={c,2c,c) ou na versão normalizada
x (3) = 
Pode ser visto que X (1) X (2)
= ab-ab= 0, x (1) x (3)
= ac-ac= 0, x (2) x (3)
= bc- 2bc + bc= 0. Assim, os autovetores desta matriz são ortogonais aos pares.
Aula 10
Formas quadráticas e sua ligação com matrizes simétricas. Propriedades de autovetores e autovalores de uma matriz simétrica. Redução de uma forma quadrática a uma forma canônica.
Definição 10.1.forma quadrática variáveis reais x 1, x 2,…, xné chamado um polinômio de segundo grau com relação a essas variáveis, que não contém um termo livre e termos de primeiro grau.
Exemplos de formas quadráticas:
(n = 2),
(n = 3). (10.1)
Lembre-se da definição de uma matriz simétrica dada na última aula:
Definição 10.2. A matriz quadrada é chamada simétrico, se , ou seja, se os elementos da matriz simétricos em relação à diagonal principal são iguais.
Propriedades de autovalores e autovetores de uma matriz simétrica:
1) Todos os autovalores de uma matriz simétrica são reais.
Prova (para n = 2).
Deixe a matriz MAS parece: 
. Vamos fazer a equação característica:
(10.2) Encontre o discriminante:
Portanto, a equação tem apenas raízes reais.
2) Os autovetores de uma matriz simétrica são ortogonais.
Prova (para n= 2).
As coordenadas dos autovetores e devem satisfazer as equações.
". A primeira parte descreve as provisões que são minimamente necessárias para a compreensão da quimiometria, e a segunda parte contém os fatos que você precisa saber para uma compreensão mais profunda dos métodos de análise multivariada. A apresentação é ilustrada por exemplos feitos em uma pasta de trabalho do Excel Matrix.xls que acompanha este documento.
Links para exemplos são colocados no texto como objetos do Excel. Esses exemplos são de natureza abstrata, não estão vinculados a tarefas de forma alguma. química Analítica. Exemplos reais o uso da álgebra matricial em quimiometria é discutido em outros textos dedicados a várias aplicações quimiométricas.
A maioria das medições realizadas em química analítica não são diretas, mas indireto. Isso significa que no experimento, em vez do valor do analito C desejado (concentração), outro valor é obtido x(sinal) relacionado, mas não igual a C, ou seja x(C) ≠ C. Via de regra, o tipo de dependência x(C) não é conhecido, mas felizmente em química analítica a maioria das medições é proporcional. Isso significa que, à medida que a concentração de C em uma vezes, o sinal X aumentará na mesma quantidade., ou seja, x(uma C) = um x(C). Além disso, os sinais também são aditivos, então o sinal de uma amostra contendo duas substâncias com concentrações de C 1 e C 2 será é igual à soma sinais de cada componente, ou seja, x(C1 + C2) = x(C1)+ x(C2). Proporcionalidade e aditividade juntas dão linearidade. Muitos exemplos poderiam ser dados para ilustrar o princípio da linearidade, mas basta mencionar os dois mais exemplos claros- cromatografia e espectroscopia. A segunda característica inerente ao experimento em química analítica é multicanal. Equipamentos analíticos modernos medem simultaneamente sinais para muitos canais. Por exemplo, a intensidade da transmissão de luz é medida para vários comprimentos de onda ao mesmo tempo, ou seja, espectro. Portanto, no experimento estamos lidando com uma variedade de sinais x 1 , x 2 ,...., x n caracterizando o conjunto de concentrações C 1 ,C 2 , ..., C m das substâncias presentes no sistema em estudo.
Arroz. 1 espectro
Assim, o experimento analítico é caracterizado pela linearidade e multidimensionalidade. Portanto, é conveniente considerar os dados experimentais como vetores e matrizes e manipulá-los usando o aparato da álgebra matricial. A frutificação dessa abordagem é ilustrada pelo exemplo mostrado em , que mostra três espectros tomados para 200 comprimentos de onda de 4.000 a 4.796 cm–1. O primeiro ( x 1) e segundo ( x 2) os espectros foram obtidos para amostras padrão nas quais as concentrações de duas substâncias A e B são conhecidas: na primeira amostra [A] = 0,5, [B] = 0,1, e na segunda amostra [A] = 0,2, [ B] = 0,6. O que pode ser dito sobre uma amostra nova e desconhecida, cujo espectro é indicado x 3 ?
Considere três espectros experimentais x 1 , x 2 e x 3 como três vetores de dimensão 200. Usando álgebra linear, pode-se mostrar facilmente que x 3 = 0.1 x 1 +0.3 x 2 , então a terceira amostra obviamente contém apenas substâncias A e B em concentrações [A] = 0,5×0,1 + 0,2×0,3 = 0,11 e [B] = 0,1×0,1 + 0,6×0,3 = 0,19.
Matriz chamado de tabela retangular de números, por exemplo
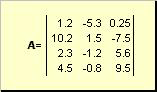
Arroz. 2 Matriz
As matrizes são indicadas por letras maiúsculas em negrito ( UMA), e seus elementos - correspondentes minúsculas com índices, ou seja, uma eu j . O primeiro índice numera as linhas e o segundo numera as colunas. Em quimiometria, costuma-se designar o valor máximo do índice com a mesma letra do próprio índice, mas em maiúsculas. Portanto, a matriz UMA também pode ser escrito como ( uma eu j , eu = 1,..., EU; j = 1,..., J). Para a matriz de exemplo EU = 4, J= 3 e uma 23 = −7.5.
par de números EU e Jé chamado de dimensão da matriz e é denotado como EU× J. Um exemplo de matriz em quimiometria é um conjunto de espectros obtidos para EU amostras em J comprimentos de onda.
As matrizes podem multiplicar por números. Nesse caso, cada elemento é multiplicado por esse número. Por exemplo -
Arroz. 3 Multiplicando uma matriz por um número
Duas matrizes de mesma dimensão podem ser elementares dobrar e subtrair. Por exemplo,
Arroz. 4 adição de matriz
Como resultado da multiplicação por um número e adição, obtém-se uma matriz de mesma dimensão.
Uma matriz zero é uma matriz composta por zeros. É designado O. É óbvio que UMA+O = UMA, UMA−UMA = O e 0 UMA = O.
A matriz pode transpor. Durante esta operação, a matriz é invertida, ou seja, linhas e colunas são trocadas. A transposição é indicada por um traço, UMA" ou índice UMA t. Assim, se UMA = {uma eu j , eu = 1,..., EU; j = 1,...,J), então UMA t = ( uma ji , j = 1,...,J; i = 1,..., EU). Por exemplo
Arroz. 5 Transposição de matriz
É óbvio que ( UMA t) t = UMA, (UMA+B) t = A+ B t.
As matrizes podem multiplicar, mas apenas se tiverem as dimensões apropriadas. Por que isso é assim ficará claro a partir da definição. Produto de matriz UMA, dimensão EU× K, e matrizes B, dimensão K× J, é chamada de matriz C, dimensão EU× J, cujos elementos são números
Assim para o produto ABé necessário que o número de colunas na matriz esquerda UMA era igual ao número de linhas na matriz direita B. Exemplo de produto de matriz -
Fig.6 Produto de matrizes
A regra de multiplicação de matrizes pode ser formulada como segue. Para encontrar um elemento de uma matriz C parado no cruzamento eu-ésima linha e j-ésima coluna ( c eu j) deve ser multiplicado elemento por elemento eu-ésima linha da primeira matriz UMA no j-ésima coluna da segunda matriz B e some todos os resultados. Assim, no exemplo mostrado, o elemento da terceira linha e da segunda coluna é obtido como a soma dos produtos elementares da terceira linha UMA e segunda coluna B
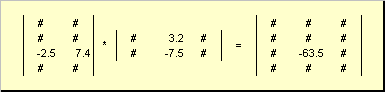
Fig.7 Elemento do produto de matrizes
O produto de matrizes depende da ordem, ou seja, AB ≠ BA, pelo menos por razões dimensionais. Diz-se que não é comutativo. No entanto, o produto de matrizes é associativo. Significa que abc = (AB)C = UMA(BC). Além disso, também é distributivo, ou seja, UMA(B+C) = AB+CA. É óbvio que AO = O.
Se o número de colunas de uma matriz for igual ao número de suas linhas ( EU = J=N), então essa matriz é chamada de quadrado. Nesta seção, consideraremos apenas essas matrizes. Dentre essas matrizes, pode-se destacar matrizes com propriedades especiais.
Solitário matriz (indicada EU e às vezes E) é uma matriz em que todos os elementos são iguais a zero, exceto os diagonais, que são iguais a 1, ou seja.
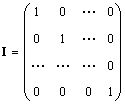
Obviamente IA = I A = UMA.
A matriz é chamada diagonal, se todos os seus elementos, exceto os diagonais ( uma ii) são iguais a zero. Por exemplo
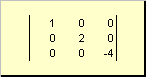
Arroz. 8 Matriz diagonal
Matriz UMA chamado de topo triangular, se todos os seus elementos situados abaixo da diagonal são iguais a zero, ou seja. uma eu j= 0, em eu>j. Por exemplo
Arroz. 9 Matriz triangular superior
A matriz triangular inferior é definida de forma semelhante.
Matriz UMA chamado simétrico, E se UMA t = UMA. Em outras palavras uma eu j = uma ji. Por exemplo
Arroz. 10 Matriz simétrica
Matriz UMA chamado ortogonal, E se
UMA t UMA = AA t = EU.
A matriz é chamada normal E se
Seguindo matriz quadrada UMA(denominado Tr( UMA) ou Sp( UMA)) é a soma de seus elementos diagonais,
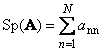
Por exemplo,
Arroz. 11 Traço de matriz
É óbvio que
Sp(α UMA) = α Sp( UMA) e
Sp( UMA+B) = Sp( UMA)+ Sp( B).
Pode ser mostrado que
Sp( UMA) = Sp( UMA t), Sp( EU) = N,
e também que
Sp( AB) = Sp( BA).
Outra característica importante de uma matriz quadrada é sua determinante(indicado por det( UMA)). A definição do determinante em caso Geral bastante complicado, então vamos começar com a opção mais simples - a matriz UMA dimensão (2×2). Então
Para uma matriz (3×3), o determinante será igual a
No caso de uma matriz ( N× N) o determinante é calculado como a soma 1 2 3 ... N= N! termos, cada um dos quais é igual a
Índices k 1 , k 2 ,..., kN são definidos como todas as permutações ordenadas possíveis r números no conjunto (1, 2, ... , N). O cálculo do determinante da matriz é um procedimento complexo, que na prática é realizado usando programas especiais. Por exemplo,
Arroz. 12 Determinante da matriz
Observamos apenas as propriedades óbvias:
det( EU) = 1, det( UMA) = det( UMA t),
det( AB) = det( UMA)det( B).
Se a matriz tiver apenas uma coluna ( J= 1), então tal objeto é chamado vetor. Mais precisamente, um vetor coluna. Por exemplo
Matrizes que consistem em uma linha também podem ser consideradas, por exemplo
Este objeto também é um vetor, mas vetor de linha. Ao analisar os dados, é importante entender com quais vetores estamos lidando - colunas ou linhas. Assim, o espectro tomado para uma amostra pode ser considerado como um vetor de linha. Então o conjunto de intensidades espectrais em algum comprimento de onda para todas as amostras deve ser tratado como um vetor coluna.
A dimensão de um vetor é o número de seus elementos.
É claro que qualquer vetor coluna pode ser transformado em um vetor linha por transposição, ou seja,
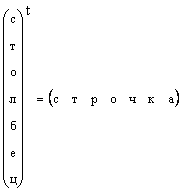
Nos casos em que a forma de um vetor não é especificada especificamente, mas simplesmente um vetor é dito, então eles significam um vetor coluna. Também vamos aderir a esta regra. Um vetor é indicado por uma letra minúscula em negrito direto. Um vetor zero é um vetor cujos elementos são iguais a zero. é denotado 0 .
Os vetores podem ser somados e multiplicados por números da mesma forma que as matrizes. Por exemplo,
Arroz. 13 Operações com vetores
Dois vetores x e y chamado colinear, se existe um número α tal que
Dois vetores de mesma dimensão N pode ser multiplicado. Sejam dois vetores x = (x 1 , x 2 ,...,x N) t e y = (y 1 , y 2 ,...,y N) t. Guiados pela regra de multiplicação "linha por coluna", podemos fazer dois produtos a partir deles: x t y e xy t. Primeiro trabalho
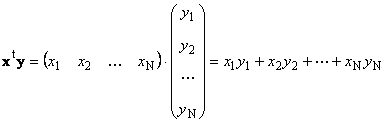
chamado escalar ou interno. Seu resultado é um número. Ele também usa a notação ( x,y)= x t y. Por exemplo,
Arroz. 14 Produto interno (escalar)
Segundo trabalho
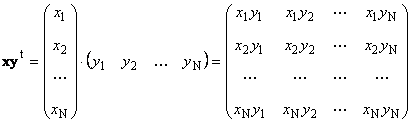
chamado externo. Seu resultado é uma matriz de dimensão ( N× N). Por exemplo,
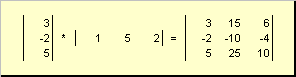
Arroz. 15 Produto externo
Vetores, produto escalar que é igual a zero são chamados ortogonal.
O produto escalar de um vetor consigo mesmo é chamado de quadrado escalar. Este valor
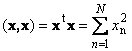
define um quadrado comprimento vetor x. Para denotar comprimento (também chamado a norma vetor) a notação é usada
Por exemplo,
Arroz. 16 Norma vetorial
Vetor de comprimento unitário (|| x|| = 1) é chamado de normalizado. Vetor diferente de zero ( x ≠ 0 ) pode ser normalizado dividindo-o pelo comprimento, ou seja, x = ||x|| (x/||x||) = ||x|| e. Aqui e = x/||x|| é um vetor normalizado.
Os vetores são chamados ortonormais se forem todos normalizados e ortogonais aos pares.
O produto escalar define e cantoφ entre dois vetores x e y
Se os vetores são ortogonais, então cosφ = 0 e φ = π/2, e se eles são colineares, então cosφ = 1 e φ = 0.
Cada matriz UMA Tamanho EU× J pode ser representado como um conjunto de vetores
Aqui cada vetor uma jé j-th coluna e vetor de linha b eué eu-ésima linha da matriz UMA
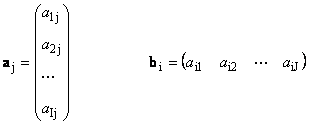
Vetores de mesma dimensão ( N) pode ser adicionado e multiplicado por um número, assim como as matrizes. O resultado é um vetor de mesma dimensão. Sejam vários vetores de mesma dimensão x 1 , x 2 ,...,x K e o mesmo número de números α α 1 , α 2 ,...,α K. Vetor
y= α1 x 1 + α2 x 2 +...+α K x K
chamado combinação linear vetores x k .
Se houver tais números diferentes de zero α k ≠ 0, k = 1,..., K, o que y = 0 , então tal conjunto de vetores x k chamado linearmente dependente. Caso contrário, os vetores são chamados linearmente independentes. Por exemplo, vetores x 1 = (2, 2) te x 2 = (−1, −1) t são linearmente dependentes, uma vez que x 1 +2x 2 = 0
Considere um conjunto de K vetores x 1 , x 2 ,...,x K dimensões N. O posto deste sistema de vetores é o número máximo de vetores linearmente independentes. Por exemplo no conjunto
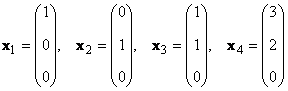
existem apenas dois vetores linearmente independentes, por exemplo x 1 e x 2 , então seu posto é 2.
Obviamente, se houver mais vetores no conjunto do que sua dimensão ( K>N), então eles são necessariamente linearmente dependentes.
Classificação da matriz(indicado por classificação ( UMA)) é o posto do sistema de vetores em que consiste. Embora qualquer matriz possa ser representada de duas maneiras (vetores de coluna ou vetores de linha), isso não afeta o valor do posto, pois
matriz quadrada UMAé chamado não degenerado se tiver um único marcha ré matriz UMA-1 , determinado pelas condições
AA −1 = UMA −1 UMA = EU.
A matriz inversa não existe para todas as matrizes. Uma condição necessária e suficiente para a não degeneração é
det( UMA) ≠ 0 ou classificação( UMA) = N.
A inversão de matrizes é um procedimento complexo para o qual existem programas especiais. Por exemplo,
Arroz. 17 Inversão de matriz
Damos fórmulas para o caso mais simples - matrizes 2 × 2
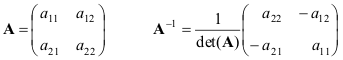
Se as matrizes UMA e B não são degenerados, então
(AB) −1 = B −1 UMA −1 .
Se a matriz UMAé degenerado e matriz inversa não existe, em alguns casos você pode usar pseudo-inverso matriz, que é definida como tal matriz UMA+ isso
AA + UMA = UMA.
A matriz pseudo-inversa não é a única e sua forma depende do método de construção. Por exemplo, para uma matriz retangular, você pode usar o método Moore-Penrose.
Se o número de colunas for menor que o número de linhas, então
UMA + =(UMA t UMA) −1 UMA t
Por exemplo,
Arroz. 17a Inversão de pseudomatriz
Se o número de colunas mais número linhas, então
UMA + =UMA t ( AA t) −1
Vetor x pode ser multiplicado por uma matriz UMA dimensão adequada. Neste caso, o vetor coluna é multiplicado à direita Machado, e a string vetorial está à esquerda x t UMA. Se a dimensão do vetor J, e a dimensão da matriz EU× J então o resultado é um vetor de dimensão EU. Por exemplo,
Arroz. 18 Multiplicação Vetorial-Matriz
Se a matriz UMA- quadrado ( EU× EU), então o vetor y = Machado tem as mesmas dimensões que x. É óbvio que
UMA(α 1 x 1 + α2 x 2) = α1 Machado 1 + α2 Machado 2 .
Portanto, as matrizes podem ser consideradas como transformações lineares de vetores. Em particular x = x, Boi = 0 .
Deixar UMA- tamanho da matriz EU× J, uma b- vetor de dimensão J. Considere a equação
Machado = b
em relação ao vetor x, dimensões EU. Essencialmente, trata-se de um sistema de EU equações lineares com J desconhecido x 1 ,...,x J. Existe uma solução se e somente se
classificação( UMA) = classificação( B) = R,
Onde Bé a matriz de dimensão aumentada EU×( J+1) que consiste na matriz UMA, acolchoado com uma coluna b, B = (UMA b). Caso contrário, as equações são inconsistentes.
Se um R = EU = J, então a solução é única
x = UMA −1 b.
Se um R < EU, então são muitos várias soluções, que pode ser expresso em termos de uma combinação linear J−R vetores. Sistema de equações homogêneas Machado = 0 com uma matriz quadrada UMA (N× N) tem uma solução não trivial ( x ≠ 0 ) se e somente se det( UMA) = 0. Se R= classificação( UMA)<N, então existem N−R soluções linearmente independentes.
Se um UMA- isto é matriz quadrada, uma x e y- vetores da dimensão correspondente, então o produto escalar da forma x t Sim chamado bilinear a forma definida pela matriz UMA. No x = y expressão x t Machado chamado quadrático Formato.
matriz quadrada UMA chamado Positivo definitivo, se para qualquer vetor diferente de zero x ≠ 0 ,
x t Machado > 0.
o negativo (x t Machado < 0), não negativo (x t Machado≥ 0) e não positivo (x t Machado≤ 0) certas matrizes.
Se a matriz simétrica UMAé definida positiva, então existe uma única matriz triangular você com elementos positivos, para os quais
UMA = você t você.
Por exemplo,
Arroz. 19 Decomposição de Cholesky
Deixar UMAé uma matriz quadrada não degenerada de dimensão N× N. Então há um único polar atuação
UMA = SR,
Onde Sé uma matriz simétrica não negativa, e Ré uma matriz ortogonal. matrizes S e R pode ser definido explicitamente:
S 2 = AA t ou S = (AA t) ½ e R = S −1 UMA = (AA t) −½ UMA.
Por exemplo,
Arroz. 20 Decomposição polar
Se a matriz UMAé degenerado, então a decomposição não é única - a saber: S ainda sozinho, mas R pode haver muitos. A decomposição polar representa uma matriz UMA como uma combinação de compressão/estiramento S e virando R.
Deixar UMAé uma matriz quadrada. Vetor v chamado próprio vetor matrizes UMA, E se
Av = λ v,
onde o número λ é chamado autovalor matrizes UMA. Assim, a transformação que a matriz realiza UMA sobre vetor v, é reduzido a um simples alongamento ou compressão com um fator λ. O autovetor é determinado até a multiplicação pela constante α ≠ 0, ou seja. E se vé um autovetor, então α v também é um autovetor.
Na matriz UMA, dimensão ( N× N) não pode ser maior que N autovalores. Eles satisfazem equação característica
det( UMA − λ EU) = 0,
ser equação algébrica N-ª ordem. Em particular, para uma matriz 2×2, a equação característica tem a forma
Por exemplo,
Arroz. 21 Autovalores
Conjunto de autovalores λ 1 ,..., λ N matrizes UMA chamado espectro UMA.
O espectro tem várias propriedades. Em particular
det( UMA) = λ 1×...×λ N, Sp( UMA) = λ 1 +...+λ N.
Os autovalores de uma matriz arbitrária podem ser números complexos, mas se a matriz for simétrica ( UMA t = UMA), então seus autovalores são reais.
Na matriz UMA, dimensão ( N× N) não pode ser maior que N autovetores, cada um dos quais corresponde ao seu próprio valor. Para determinar o autovetor v n você precisa resolver um sistema de equações homogêneas
(UMA − λ n EU)v n = 0 .
Tem uma solução não trivial porque det( UMA-λ n EU) = 0.
Por exemplo,
Arroz. 22 autovetores
Os autovetores de uma matriz simétrica são ortogonais.
