Con la matrice A, se esiste un numero l tale che AX = lX.
In questo caso, viene chiamato il numero l autovalore operatore (matrice A) corrispondente al vettore X.
In altre parole, un autovettore è un vettore che, sotto l'azione di un operatore lineare, si trasforma in un vettore collineare, cioè basta moltiplicare per un numero. Al contrario, i vettori impropri sono più difficili da trasformare.
Scriviamo la definizione di autovettore come sistema di equazioni:
Spostiamo tutti i termini sul lato sinistro:
L'ultimo sistema può essere scritto in forma matriciale come segue:
(A - lE)X \u003d O
Il sistema risultante ha sempre una soluzione zero X = O. Si chiamano tali sistemi in cui tutti i termini liberi sono uguali a zero omogeneo. Se la matrice di un tale sistema è quadrata e il suo determinante non è uguale a zero, allora dalle formule di Cramer otteniamo sempre unica decisione- zero. Si può dimostrare che il sistema ha soluzioni diverse da zero se e solo se il determinante di questa matrice è uguale a zero, cioè
|A - LE| = 
= 0
Questa equazione con l incognita è chiamata equazione caratteristica (polinomio caratteristico) matrice A (operatore lineare).
Si può dimostrare che il polinomio caratteristico di un operatore lineare non dipende dalla scelta della base.
Ad esempio, troviamo gli autovalori e gli autovettori dell'operatore lineare dati dalla matrice A = .
Per fare ciò, componiamo l'equazione caratteristica |А - lЕ| = 
\u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; autovalori l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.
Per trovare gli autovettori risolviamo due sistemi di equazioni
(LA + 5E) X = O
(LA - 7E) X = O
Per il primo di essi, la matrice espansa assumerà la forma
,
da cui x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, ad es. X (1) \u003d (- (2/3) s; s).
Per il secondo, la matrice espansa assumerà la forma
,
da cui x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, ad es. X (2) \u003d ((2/3) s 1; s 1).
Pertanto, gli autovettori di questo operatore lineare sono tutti vettori della forma (-(2/3)c; c) con autovalore (-5) e tutti i vettori della forma ((2/3)c 1 ; c 1) con autovalore 7 .
Si può dimostrare che la matrice dell'operatore A nella base costituita dai suoi autovettori è diagonale ed ha la forma:
,
dove l i sono gli autovalori di questa matrice.
È vero anche il contrario: se la matrice A in qualche base è diagonale, allora tutti i vettori di questa base saranno autovettori di questa matrice.
Si può anche dimostrare che se un operatore lineare ha n autovalori distinti a coppie, gli autovettori corrispondenti sono linearmente indipendenti e la matrice di questo operatore nella base corrispondente ha una forma diagonale.
Spieghiamolo con l'esempio precedente. Prendiamo arbitrariamente valori diversi da zero c e c 1 , ma tali che i vettori X (1) e X (2) siano linearmente indipendenti, cioè formerebbe una base. Ad esempio, lascia c \u003d c 1 \u003d 3, quindi X (1) \u003d (-2; 3), X (2) \u003d (2; 3).
Verifichiamo l'indipendenza lineare di questi vettori:
12 ≠ 0. In questa nuova base, la matrice A assumerà la forma A * = .
Per verificarlo, utilizziamo la formula A * = C -1 AC. Troviamo prima C -1.
C -1 = 
;
forma quadratica f (x 1, x 2, x n) da n variabili è chiamata somma, ogni termine della quale è o il quadrato di una delle variabili, oppure il prodotto di due diverse variabili, prese con un certo coefficiente: f (x 1 , x 2, x n) = 
(un ij = un ji).
Si chiama la matrice A, composta da questi coefficienti matrice forma quadratica. È sempre simmetrico matrice (cioè una matrice simmetrica rispetto alla diagonale principale, a ij = a ji).
Nella notazione matriciale, la forma quadratica ha la forma f(X) = X T AX, dove
Infatti
Ad esempio, scriviamo la forma quadratica in forma matriciale.
Per fare ciò, troviamo una matrice di forma quadratica. I suoi elementi diagonali sono uguali ai coefficienti ai quadrati delle variabili e gli elementi rimanenti sono uguali alla metà dei coefficienti corrispondenti della forma quadratica. Ecco perchè
Sia ottenuta la colonna-matrice delle variabili X mediante una trasformazione lineare non degenerata della colonna-matrice Y, cioè X = CY, dove C è una matrice non degenerata di ordine n. Quindi la forma quadratica f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.
Pertanto, sotto una trasformazione lineare non degenerata C, la matrice della forma quadratica assume la forma: A * = C T AC.
Ad esempio, troviamo la forma quadratica f(y 1, y 2) ottenuta dalla forma quadratica f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 mediante una trasformazione lineare.
Viene chiamata la forma quadratica canonico(Esso ha visione canonica) se tutti i suoi coefficienti a ij = 0 per i ≠ j, cioè
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.
La sua matrice è diagonale.
Teorema(la prova non è data qui). Qualsiasi forma quadratica può essere ridotta a una forma canonica utilizzando una trasformazione lineare non degenerata.
Per esempio, riduciamo alla forma canonica la forma quadratica
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
Per fare ciò, seleziona prima il quadrato intero per la variabile x 1:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.
Ora selezioniamo il quadrato intero per la variabile x 2:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.
Quindi la trasformazione lineare non degenerata y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 e y 3 \u003d x 3 porta questa forma quadratica alla forma canonica f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .
Si noti che la forma canonica di una forma quadratica è definita in modo ambiguo (la stessa forma quadratica può essere ridotta alla forma canonica diversi modi). in ogni caso, il diversi modi le forme canoniche hanno un numero proprietà comuni. In particolare, il numero di termini con coefficienti positivi (negativi) di una forma quadratica non dipende da come la forma viene ridotta a questa forma (ad esempio, nell'esempio considerato ci saranno sempre due coefficienti negativi e uno positivo). Questa proprietà è chiamata legge di inerzia delle forme quadratiche.
Verifichiamo ciò riducendo in modo diverso la stessa forma quadratica alla forma canonica. Iniziamo la trasformazione con la variabile x 2:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, dove y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 e y 3 = x 1 . Qui, un coefficiente negativo -3 a y 1 e due coefficienti positivi 3 e 2 a y 2 e y 3 (e usando un altro metodo, abbiamo ottenuto un coefficiente negativo (-5) a y 2 e due coefficienti positivi: 2 a y 1 e 1/20 per y 3).
Va anche notato che il rango di una matrice di forma quadratica, chiamato il rango della forma quadratica, è uguale al numero coefficienti diversi da zero della forma canonica e non cambia nelle trasformazioni lineari.
Viene chiamata la forma quadratica f(X). positivamente (negativo) certo, se per tutti i valori delle variabili che non sono contemporaneamente uguali a zero, è positivo, cioè f(X) > 0 (negativo, cioè
f(X)< 0).
Ad esempio, la forma quadratica f 1 (X) \u003d x 1 2 + x 2 2 è definita positiva, perché è la somma dei quadrati e la forma quadratica f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 è definita negativa, perché rappresenta può essere rappresentato come f 2 (X) \u003d - (x 1 - x 2) 2.
Nella maggior parte delle situazioni pratiche, è un po' più difficile stabilire la definizione di segno di una forma quadratica, quindi per questo viene utilizzato uno dei seguenti teoremi (li formuliamo senza dimostrazioni).
Teorema. Una forma quadratica è definita positiva (negativa) se e solo se tutti gli autovalori della sua matrice sono positivi (negativi).
Teorema(Criterio di Silvestro). Una forma quadratica è definita positiva se e solo se tutti i principali minori della matrice di questa forma sono positivi.
Maggiore (angolo) minore Il k-esimo ordine della matrice A dell'n-esimo ordine è detto determinante della matrice, composto dalle prime k righe e colonne della matrice A ().
Si noti che per le forme quadratiche definite negative, i segni dei minori principali si alternano e il minore di primo ordine deve essere negativo.
Ad esempio, esaminiamo la forma quadratica f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 per la definizione del segno.
= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17; 
. Pertanto, la forma quadratica è definita positiva.
Metodo 2. La minore maggiore del primo ordine della matrice A D 1 = a 11 = 2 > 0. La minore maggiore del secondo ordine D 2 = = 6 - 4 = 2 > 0. Pertanto, secondo il criterio di Silvestro, la forma quadratica è definita positiva.
Esaminiamo un'altra forma quadratica per la definizione dei segni, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Metodo 1. Costruiamo una matrice di forma quadratica А = . L'equazione caratteristica avrà la forma 
= (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17; 
. Pertanto, la forma quadratica è definita negativa.
Metodo 2. La maggiore minore del primo ordine della matrice A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Pertanto, secondo il criterio di Silvestro, la forma quadratica è definita negativa (i segni dei minori principali si alternano, partendo da meno).
E come altro esempio, esaminiamo la forma quadratica f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 per la definizione del segno.
Metodo 1. Costruiamo una matrice di forma quadratica А = . L'equazione caratteristica avrà la forma 
= (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41; 
.
Uno di questi numeri è negativo e l'altro è positivo. I segni degli autovalori sono diversi. Pertanto, una forma quadratica non può essere definita né negativa né positiva, cioè questa forma quadratica non è segno-definita (può assumere valori di qualsiasi segno).
Metodo 2. La minore maggiore del primo ordine della matrice A D 1 = a 11 = 2 > 0. La minore maggiore del secondo ordine D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
Un autovettore di una matrice quadrata è quello che, moltiplicato per una data matrice, risulta in un vettore collineare. In parole semplici, quando una matrice viene moltiplicata per un autovettore, quest'ultimo rimane lo stesso, ma moltiplicato per un certo numero.
Un autovettore è un vettore V diverso da zero, che moltiplicato per una matrice quadrata M diventa esso stesso, aumentato di un certo numero λ. A notazione algebrica sembra:
M × V = λ × V,
dove λ è un autovalore della matrice M.
Consideriamo un esempio numerico. Per comodità di scrittura, i numeri nella matrice saranno separati da un punto e virgola. Diciamo di avere una matrice:
Moltiplichiamolo per un vettore colonna:
Quando moltiplichiamo una matrice per un vettore colonna, otteniamo anche un vettore colonna. In un linguaggio matematico rigoroso, la formula per moltiplicare una matrice 2 × 2 per un vettore colonna sarebbe simile a questa:
M11 indica l'elemento della matrice M, che si trova nella prima riga e nella prima colonna, e M22 è l'elemento che si trova nella seconda riga e nella seconda colonna. Per la nostra matrice, questi elementi sono M11 = 0, M12 = 4, M21 = 6, M22 10. Per un vettore colonna, questi valori sono V11 = –2, V21 = 1. Secondo questa formula, otteniamo quanto segue risultato del prodotto di una matrice quadrata per un vettore:
Per comodità, scriviamo il vettore colonna in una riga. Quindi, abbiamo moltiplicato la matrice quadrata per il vettore (-2; 1), ottenendo il vettore (4; -2). Ovviamente, questo è lo stesso vettore moltiplicato per λ = -2. lambda dentro questo caso denota un autovalore della matrice.
L'autovettore di una matrice è un vettore collineare, cioè un oggetto che non cambia posizione nello spazio quando viene moltiplicato per una matrice. Il concetto di collinearità nell'algebra vettoriale è simile al termine di parallelismo in geometria. Nell'interpretazione geometrica, i vettori collineari sono segmenti diretti paralleli lunghezze diverse. Dai tempi di Euclide sappiamo che una singola retta ha un numero infinito di rette parallele, quindi è logico supporre che ogni matrice abbia un numero infinito di autovettori.
Dall'esempio precedente, si può vedere che entrambi (-8; 4), e (16; -8), e (32, -16) possono essere autovettori. Tutti questi sono vettori collineari corrispondenti all'autovalore λ = -2. Quando moltiplichiamo la matrice originale per questi vettori, otterremo comunque un vettore, che differisce dall'originale di 2 volte. Ecco perché, quando si risolvono problemi per trovare un autovettore, è necessario trovare solo oggetti vettoriali linearmente indipendenti. Molto spesso, per una matrice n × n, esiste un numero n-esimo di autovettori. Il nostro calcolatore è progettato per l'analisi di matrici quadrate del secondo ordine, quindi quasi sempre si troveranno come risultato due autovettori, tranne quando coincidono.
Nell'esempio sopra, conoscevamo in anticipo l'autovettore della matrice originale e determinavamo visivamente il numero lambda. In pratica, però, tutto accade al contrario: all'inizio c'è autovalori e solo allora gli autovettori.
Esaminiamo nuovamente la matrice originale M e proviamo a trovare entrambi i suoi autovettori. Quindi la matrice si presenta come:
Per cominciare, dobbiamo determinare l'autovalore λ, per il quale dobbiamo calcolare il determinante della seguente matrice:
Questa matrice si ottiene sottraendo l'incognita λ dagli elementi sulla diagonale principale. Il determinante è determinato dalla formula standard:
Poiché il nostro vettore non deve essere zero, prendiamo l'equazione risultante come linearmente dipendente e uguagliamo il nostro determinante detA a zero.
(0 - λ) × (10 - λ) - 24 = 0
Apriamo le parentesi e otteniamo l'equazione caratteristica della matrice:
λ 2 − 10 λ − 24 = 0
Questo è standard equazione quadrata, che va risolta in termini di discriminante.
D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196
La radice del discriminante è sqrt(D) = 14, quindi λ1 = -2, λ2 = 12. Ora per ogni valore lambda, dobbiamo trovare un autovettore. Esprimiamo i coefficienti del sistema per λ = -2.
In questa formula, E è matrice identità. Sulla base della matrice ottenuta, componiamo un sistema di equazioni lineari:
2x + 4 anni = 6x + 12 anni
dove xey sono elementi dell'autovettore.
Raccogliamo tutte le X a sinistra e tutte le Y a destra. Ovviamente - 4x = 8y. Dividi l'espressione per -4 e ottieni x = -2y. Ora possiamo determinare il primo autovettore della matrice prendendo qualsiasi valore delle incognite (ricordate l'infinito di autovettori linearmente dipendenti). Prendiamo y = 1, quindi x = -2. Pertanto, il primo autovettore appare come V1 = (–2; 1). Torna all'inizio dell'articolo. È stato questo oggetto vettoriale per il quale abbiamo moltiplicato la matrice per dimostrare il concetto di autovettore.
Ora troviamo l'autovettore per λ = 12.
Componiamo lo stesso sistema di equazioni lineari;
Ora prendiamo x = 1, quindi y = 3. Quindi, il secondo autovettore appare come V2 = (1; 3). Quando si moltiplica la matrice originale per questo vettore, il risultato sarà sempre lo stesso vettore moltiplicato per 12. Questo completa l'algoritmo di soluzione. Ora sai come definire manualmente un autovettore di una matrice.
Il programma opera secondo l'algoritmo di cui sopra, riducendo al minimo il processo di soluzione. È importante sottolineare che nel programma la lambda è indicata dalla lettera "c". Diamo un'occhiata a un esempio numerico.
Proviamo a definire gli autovettori per la seguente matrice:
Inseriamo questi valori nelle celle della calcolatrice e otteniamo la risposta nel seguente modulo:
Pertanto, abbiamo ottenuto due autovettori linearmente indipendenti.
L'algebra lineare e la geometria analitica sono materie standard per qualsiasi matricola in ingegneria. Un gran numero di vettori e matrici è terrificante, ed è facile sbagliare in calcoli così ingombranti. Il nostro programma consentirà agli studenti di verificare i propri calcoli o di risolvere automaticamente il problema della ricerca di un autovettore. Ci sono altri calcolatori di algebra lineare nel nostro catalogo, usali nel tuo studio o lavoro.
Come inserire formule matematiche nel sito?
Se hai bisogno di aggiungere una o due formule matematiche a una pagina web, il modo più semplice per farlo è come descritto nell'articolo: le formule matematiche si inseriscono facilmente nel sito sotto forma di immagini che Wolfram Alpha genera automaticamente. Oltre alla semplicità, questo metodo universale aiuterà a migliorare la visibilità del sito in motori di ricerca. Funziona da molto tempo (e penso che funzionerà per sempre), ma è moralmente obsoleto.
Se utilizzi costantemente formule matematiche sul tuo sito, ti consiglio di utilizzare MathJax, una speciale libreria JavaScript che visualizza la notazione matematica nei browser Web utilizzando il markup MathML, LaTeX o ASCIIMathML.
Ci sono due modi per iniziare a usare MathJax: (1) usando un semplice codice, puoi collegare velocemente uno script MathJax al tuo sito, che verrà caricato automaticamente da un server remoto al momento giusto (elenco dei server); (2) carica lo script MathJax da un server remoto sul tuo server e collegalo a tutte le pagine del tuo sito. Il secondo metodo è più complesso e richiede tempo e ti consentirà di velocizzare il caricamento delle pagine del tuo sito, e se il server principale MathJax diventa temporaneamente non disponibile per qualche motivo, ciò non influirà in alcun modo sul tuo sito. Nonostante questi vantaggi, ho scelto il primo metodo, in quanto è più semplice, veloce e non richiede competenze tecniche. Segui il mio esempio e in 5 minuti sarai in grado di utilizzare tutte le funzionalità di MathJax sul tuo sito web.
Puoi connettere lo script della libreria MathJax da un server remoto utilizzando due opzioni di codice prese dal sito Web principale di MathJax o dalla pagina della documentazione:
Una di queste opzioni di codice deve essere copiata e incollata nel codice della tua pagina web, preferibilmente tra i tag
e o subito dopo il tag . Secondo la prima opzione, MathJax si carica più velocemente e rallenta meno la pagina. Ma la seconda opzione traccia e carica automaticamente le ultime versioni di MathJax. Se inserisci il primo codice, sarà necessario aggiornarlo periodicamente. Se incolli il secondo codice, le pagine verranno caricate più lentamente, ma non dovrai monitorare costantemente gli aggiornamenti di MathJax.Il modo più semplice per connettere MathJax è in Blogger o WordPress: nel pannello di controllo del sito, aggiungi un widget progettato per inserire codice JavaScript di terze parti, copia la prima o la seconda versione del codice di caricamento sopra e posiziona il widget più vicino a l'inizio del modello (a proposito, questo non è affatto necessario, poiché lo script MathJax viene caricato in modo asincrono). È tutto. Ora impara la sintassi del markup MathML, LaTeX e ASCIIMathML e sei pronto per incorporare formule matematiche nelle tue pagine web.
Qualsiasi frattale è costruito secondo una certa regola, che viene applicata costantemente un numero illimitato di volte. Ciascuno di questi tempi è chiamato iterazione.
L'algoritmo iterativo per costruire una spugna di Menger è abbastanza semplice: il cubo originale di lato 1 è diviso da piani paralleli alle sue facce in 27 cubi uguali. Da esso vengono rimossi un cubo centrale e 6 cubi adiacenti ad esso lungo le facce. Si scopre un set composto da 20 cubi più piccoli rimanenti. Facendo lo stesso con ciascuno di questi cubi, otteniamo un set composto da 400 cubi più piccoli. Continuando questo processo all'infinito, otteniamo la spugna Menger.
Definizione 9.3. Vettore X chiamato proprio vettore matrici MA se esiste un tale numero λ, che vale l'uguaglianza: MA X= λ X, cioè il risultato dell'applicazione a X trasformazione lineare data dalla matrice MA, è la moltiplicazione di questo vettore per il numero λ . Il numero stesso λ chiamato proprio numero matrici MA.
Sostituzione nelle formule (9.3) x` j = λx j , otteniamo un sistema di equazioni per determinare le coordinate dell'autovettore:
. (9.5)
Questo lineare sistema omogeneo avrà una soluzione non banale solo se il suo determinante principale è 0 (regola di Cramer). Scrivendo questa condizione nella forma:
otteniamo un'equazione per determinare gli autovalori λ chiamato equazione caratteristica. In breve, può essere rappresentato come segue:
| A-λE | = 0, (9.6)
poiché il suo lato sinistro è il determinante della matrice A-λE. Polinomio rispetto a λ | A-λE| chiamato polinomio caratteristico matrici A.
Proprietà del polinomio caratteristico:
1) Il polinomio caratteristico di una trasformazione lineare non dipende dalla scelta della base. Prova. 
(vedi (9.4)), ma 
Di conseguenza, . Quindi, non dipende dalla scelta della base. Quindi, e | A-λE| non cambia al passaggio a una nuova base.
2) Se la matrice MA la trasformazione lineare è simmetrico(quelli. un ij = un ji), allora tutte le radici dell'equazione caratteristica (9.6) sono numeri reali.
Proprietà di autovalori e autovettori:
1) Se scegliamo una base da autovettori x 1, x 2, x 3 corrispondente agli autovalori λ 1 , λ 2 , λ 3 matrici MA, allora in questa base la trasformazione lineare A ha una matrice diagonale:
(9.7) La dimostrazione di questa proprietà deriva dalla definizione di autovettori.
2) Se la trasformazione autovalori MA sono differenti, allora gli autovettori ad essi corrispondenti sono linearmente indipendenti.
3) Se il polinomio caratteristico della matrice MA ha tre diverse radici, quindi in qualche modo la matrice MA ha una forma diagonale.
Troviamo gli autovalori e gli autovettori della matrice Facciamo l'equazione caratteristica: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7 λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
Trova le coordinate degli autovettori corrispondenti a ciascun valore trovato λ. Dalla (9.5) segue che se X (1) ={x 1, x 2, x 3) è l'autovettore corrispondente a λ 1 = -2, quindi
- articolare, ma sistema indefinito. La sua soluzione può essere scritta come X (1)
={un,0,-un), dove a è un numero qualsiasi. In particolare, se ne hai bisogno | X (1)
|=1, X (1)
=
Sostituzione nel sistema (9.5) λ 2 =3, otteniamo un sistema per determinare le coordinate del secondo autovettore - X (2) ={y1,y2,y3}:
, dove X (2)
={b,-b, b) o, a condizione | X (2)
|=1, X (2)
= 
Per λ 3 = 6 trova l'autovettore X (3) ={z1, z2, z3}:
, X (3)
={c,2c,c) o nella versione normalizzata
x (3) = 
Si può vedere che X (1) X (2)
= ab-ab= 0, X (1) X (3)
= ac-ac= 0, X (2) X (3)
= avanti Cristo- 2aC + aC= 0. Pertanto, gli autovettori di questa matrice sono ortogonali a coppie.
Lezione 10
Forme quadratiche e loro connessione con matrici simmetriche. Proprietà degli autovettori e autovalori di una matrice simmetrica. Riduzione di una forma quadratica a una forma canonica.
Definizione 10.1.forma quadratica variabili reali x 1, x 2,…, x n si chiama un polinomio di secondo grado rispetto a tali variabili, che non contiene termine libero e termini di primo grado.
Esempi di forme quadratiche:
(n = 2),
(n = 3). (10.1)
Ricordiamo la definizione di matrice simmetrica data nell'ultima lezione:
Definizione 10.2. Si chiama la matrice quadrata simmetrico, se , cioè se gli elementi della matrice simmetrici rispetto alla diagonale principale sono uguali.
Proprietà degli autovalori e degli autovettori di una matrice simmetrica:
1) Tutti gli autovalori di una matrice simmetrica sono reali.
Prova (per n = 2).
Sia la matrice MA sembra: 
. Facciamo l'equazione caratteristica:
(10.2) Trova il discriminante:
Pertanto, l'equazione ha solo radici reali.
2) Gli autovettori di una matrice simmetrica sono ortogonali.
Prova (per n= 2).
Le coordinate degli autovettori e devono soddisfare le equazioni.
". La prima parte delinea le disposizioni minimamente necessarie per comprendere la chemiometria, e la seconda parte contiene i fatti che è necessario conoscere per una comprensione più approfondita dei metodi di analisi multivariata. La presentazione è illustrata da esempi realizzati in una cartella di lavoro di Excel Matrix.xls che accompagna questo documento.
I collegamenti agli esempi vengono inseriti nel testo come oggetti di Excel. Questi esempi sono di natura astratta, non sono in alcun modo legati ai compiti. chimica analitica. Esempi reali l'uso dell'algebra delle matrici in chemiometria è discusso in altri testi dedicati a varie applicazioni chemiometriche.
La maggior parte delle misurazioni effettuate in chimica analitica non sono dirette ma indiretto. Ciò significa che nell'esperimento, invece del valore dell'analita C desiderato (concentrazione), si ottiene un altro valore X(segnale) relativo ma non uguale a C, cioè X(C) ≠ C. Di norma, il tipo di dipendenza X(C) non è noto, ma fortunatamente in chimica analitica la maggior parte delle misurazioni sono proporzionali. Ciò significa che come concentrazione di C in un volte, il segnale X aumenterà della stessa quantità., cioè X(un C) = ascia(C). Inoltre i segnali sono anche additivi, quindi il segnale di un campione contenente due sostanze con concentrazioni di C 1 e C 2 sarà è uguale alla somma segnali provenienti da ogni componente, ad es. X(C1 + C2) = X(C1)+ X(C2). Proporzionalità e additività insieme danno linearità. Si potrebbero fare molti esempi per illustrare il principio di linearità, ma basti citare i due più esempi chiari- cromatografia e spettroscopia. La seconda caratteristica inerente all'esperimento di chimica analitica è multicanale. Le moderne apparecchiature analitiche misurano simultaneamente i segnali per molti canali. Ad esempio, l'intensità della trasmissione della luce viene misurata per più lunghezze d'onda contemporaneamente, ad es. spettro. Pertanto, nell'esperimento abbiamo a che fare con una varietà di segnali X 1 , X 2 ,...., X n che caratterizza l'insieme delle concentrazioni C 1 ,C 2 , ..., C m delle sostanze presenti nel sistema in esame.
Riso. 1 Spettro
Quindi, l'esperimento analitico è caratterizzato da linearità e multidimensionalità. Pertanto, è conveniente considerare i dati sperimentali come vettori e matrici e manipolarli utilizzando l'apparato dell'algebra delle matrici. La fruttuosità di questo approccio è illustrata dall'esempio mostrato in , che mostra tre spettri presi per 200 lunghezze d'onda da 4000 a 4796 cm–1. Il primo ( X 1) e secondo ( X 2) gli spettri sono stati ottenuti per campioni standard in cui sono note le concentrazioni di due sostanze A e B: nel primo campione [A] = 0,5, [B] = 0,1, e nel secondo campione [A] = 0,2, [ B] = 0,6. Cosa si può dire di un nuovo campione sconosciuto, il cui spettro è indicato X 3 ?
Considera tre spettri sperimentali X 1 , X 2 e X 3 come tre vettori di dimensione 200. Usando l'algebra lineare, si può facilmente dimostrarlo X 3 = 0.1 X 1 +0.3 X 2 , quindi il terzo campione contiene ovviamente solo le sostanze A e B nelle concentrazioni [A] = 0.5×0.1 + 0.2×0.3 = 0.11 e [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
Matrice chiamato una tabella di numeri rettangolare, per esempio
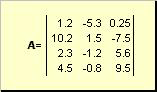
Riso. 2 Matrice
Le matrici sono indicate con lettere maiuscole in grassetto ( UN), e i loro elementi - corrispondenti minuscolo con indici, cioè un ij. Il primo indice numera le righe e il secondo numera le colonne. In chemiometria, è consuetudine designare il valore massimo dell'indice con la stessa lettera dell'indice stesso, ma in lettere maiuscole. Pertanto, la matrice UN può anche essere scritto come ( un ij , io = 1,..., io; j = 1,..., J). Per la matrice di esempio io = 4, J= 3 e un 23 = −7.5.
Coppia di numeri io e Jè chiamata dimensione della matrice ed è indicata come io× J. Un esempio di matrice in chemiometria è un insieme di spettri ottenuti per io campioni su J lunghezze d'onda.
Le matrici possono moltiplicare per numeri. In questo caso, ogni elemento viene moltiplicato per questo numero. Per esempio -
Riso. 3 Moltiplicare una matrice per un numero
Due matrici della stessa dimensione possono essere per elemento piega e sottrarre. Per esempio,
Riso. 4 Aggiunta di matrici
Come risultato della moltiplicazione per un numero e dell'addizione, si ottiene una matrice della stessa dimensione.
Una matrice zero è una matrice composta da zeri. È designato o. È ovvio che UN+o = UN, UN−UN = o e 0 UN = o.
La matrice può trasporre. Durante questa operazione, la matrice viene capovolta, ad es. righe e colonne vengono scambiate. La trasposizione è indicata da un trattino, UN" o indice UN t . Quindi, se UN = {un ij , io = 1,..., io; j = 1,...,J), poi UN t = ( un ji , j = 1,...,J; io = 1,..., io). Per esempio
Riso. 5 Trasposizione della matrice
È ovvio che ( UN t) t = UN, (UN+B) t = A t + B t .
Le matrici possono moltiplicare, ma solo se hanno le dimensioni adeguate. Perché è così sarà chiaro dalla definizione. Prodotto a matrice UN, dimensione io× K e matrici B, dimensione K× J, è chiamata matrice C, dimensione io× J, i cui elementi sono numeri
Quindi per il prodotto ABè necessario che il numero di colonne nella matrice di sinistra UN era uguale al numero di righe nella matrice di destra B. Esempio di prodotto Matrix -
Fig.6 Prodotto di matrici
La regola di moltiplicazione delle matrici può essere formulata come segue. Per trovare un elemento di una matrice C fermo all'incrocio io-esima riga e j-esima colonna ( c ij) deve essere moltiplicato elemento per elemento io-esima riga della prima matrice UN sul j-esima colonna della seconda matrice B e somma tutti i risultati. Quindi nell'esempio mostrato, l'elemento della terza riga e della seconda colonna è ottenuto come somma dei prodotti per elemento della terza riga UN e seconda colonna B
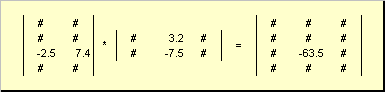
Fig.7 Elemento del prodotto delle matrici
Il prodotto delle matrici dipende dall'ordine, cioè AB ≠ BA, almeno per ragioni dimensionali. Si dice non commutativo. Tuttavia, il prodotto delle matrici è associativo. Significa che ABC = (AB)C = UN(AVANTI CRISTO). Inoltre, è anche distributivo, cioè UN(B+C) = AB+corrente alternata. È ovvio che AO = o.
Se il numero di colonne di una matrice è uguale al numero delle sue righe ( io = G=N), allora tale matrice è chiamata quadrata. In questa sezione considereremo solo tali matrici. Tra queste matrici, si possono individuare matrici con proprietà speciali.
Solitario matrice (indicata io e qualche volta e) è una matrice in cui tutti gli elementi sono uguali a zero, eccetto quelli diagonali, che sono uguali a 1, cioè
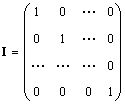
Ovviamente AI = IA = UN.
La matrice è chiamata diagonale, se tutti i suoi elementi, eccetto quelli diagonali ( un ii) sono uguali a zero. Per esempio
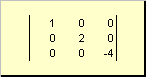
Riso. 8 Matrice diagonale
Matrice UN chiamato il top triangolare, se tutti i suoi elementi che giacciono al di sotto della diagonale sono uguali a zero, cioè un ij= 0, a io>j. Per esempio
Riso. 9 Matrice triangolare superiore
La matrice triangolare inferiore è definita in modo simile.
Matrice UN chiamato simmetrico, Se UN t = UN. In altre parole un ij = un ji. Per esempio
Riso. 10 Matrice simmetrica
Matrice UN chiamato ortogonale, Se
UN t UN = aa t = io.
La matrice è chiamata normale Se
Seguente matrice quadrata UN(indicato con Tr( UN) o Sp( UN)) è la somma dei suoi elementi diagonali,
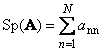
Per esempio,
Riso. 11 Traccia della matrice
È ovvio che
Sp(α UN) = α Sp( UN) e
Sp( UN+B) = Sp( UN)+ Sp( B).
Si può dimostrare che
Sp( UN) = Sp( UN t), Sp( io) = N,
e anche quello
Sp( AB) = Sp( BA).
Un'altra importante caratteristica di una matrice quadrata è la sua determinante(indicato da det( UN)). La definizione del determinante in caso generale abbastanza complicato, quindi inizieremo con l'opzione più semplice: la matrice UN dimensione (2×2). Quindi
Per una matrice (3×3), il determinante sarà uguale a
Nel caso di una matrice ( N× N) il determinante è calcolato come somma 1 2 3 ... N= N! termini, ciascuno dei quali è uguale a
Indici K 1 , K 2 ,..., k N sono definite come tutte le possibili permutazioni ordinate r numeri nell'insieme (1, 2, ... , N). Il calcolo del determinante matriciale è una procedura complessa, che in pratica viene effettuata mediante appositi programmi. Per esempio,
Riso. 12 Determinante della matrice
Notiamo solo le proprietà ovvie:
det( io) = 1, det( UN) = dettaglio( UN t),
det( AB) = dettaglio( UN)dettagli( B).
Se la matrice ha una sola colonna ( J= 1), quindi viene chiamato tale oggetto vettore. Più precisamente, un vettore colonna. Per esempio
Si possono considerare, ad esempio, anche matrici composte da una riga
Questo oggetto è anche un vettore, ma vettore di riga. Quando si analizzano i dati, è importante capire con quali vettori abbiamo a che fare: colonne o righe. Quindi lo spettro preso per un campione può essere considerato come un vettore di riga. Quindi l'insieme delle intensità spettrali a una certa lunghezza d'onda per tutti i campioni dovrebbe essere trattato come un vettore colonna.
La dimensione di un vettore è il numero dei suoi elementi.
È chiaro che qualsiasi vettore colonna può essere trasformato in un vettore riga per trasposizione, cioè
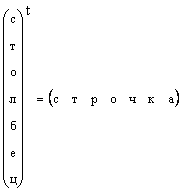
In quei casi in cui la forma di un vettore non è specificata in modo specifico, ma si dice semplicemente un vettore, allora si intende un vettore colonna. Rispetteremo anche questa regola. Un vettore è indicato da una lettera in grassetto diretta minuscola. Un vettore zero è un vettore i cui elementi sono tutti uguali a zero. È indicato 0 .
I vettori possono essere sommati e moltiplicati per numeri allo stesso modo delle matrici. Per esempio,
Riso. 13 Operazioni con i vettori
Due vettori X e y chiamato collineare, se esiste un numero α tale
Due vettori della stessa dimensione N può essere moltiplicato. Siano due vettori X = (X 1 , X 2 ,...,X N) t e y = (y 1 , y 2 ,...,y N) t . Guidati dalla regola di moltiplicazione "riga per colonna", possiamo ricavarne due prodotti: X t y e xy t . Primo lavoro
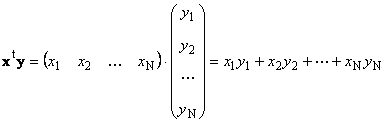
chiamato scalare o interno. Il suo risultato è un numero. Usa anche la notazione ( X,y)= X t y. Per esempio,
Riso. 14 Prodotto interno (scalare).
Secondo lavoro
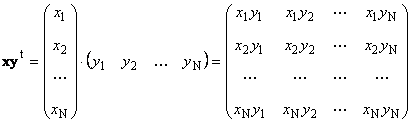
chiamato esterno. Il suo risultato è una matrice dimensionale ( N× N). Per esempio,
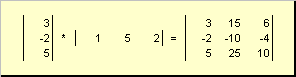
Riso. 15 Prodotto esterno
vettori, prodotto scalare che è uguale a zero vengono chiamati ortogonale.
Il prodotto scalare di un vettore con se stesso è chiamato quadrato scalare. Questo valore
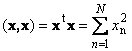
definisce un quadrato lunghezza vettore X. Per denotare la lunghezza (chiamato anche La norma vettore) viene utilizzata la notazione
Per esempio,
Riso. 16 Norma vettoriale
Vettore di lunghezza dell'unità (|| X|| = 1) è detto normalizzato. vettore diverso da zero ( X ≠ 0 ) può essere normalizzato dividendo per la lunghezza, cioè X = ||X|| (X/||X||) = ||X|| e. Qui e = X/||X|| è un vettore normalizzato.
I vettori si dicono ortonormali se sono tutti normalizzati e ortogonali a coppie.
Il prodotto scalare definisce e angoloφ tra due vettori X e y
Se i vettori sono ortogonali, allora cosφ = 0 e φ = π/2, e se sono collineari, allora cosφ = 1 e φ = 0.
Ogni matrice UN taglia io× J può essere rappresentato come un insieme di vettori
Qui ogni vettore un jè j-esima colonna e vettore di riga b ioè io-esima riga della matrice UN
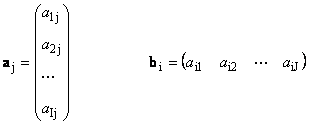
Vettori della stessa dimensione ( N) possono essere sommati e moltiplicati per un numero, proprio come le matrici. Il risultato è un vettore della stessa dimensione. Siano presenti più vettori della stessa dimensione X 1 , X 2 ,...,X K e lo stesso numero di numeri α α 1 , α 2 ,...,α K. Vettore
y= α 1 X 1 + α 2 X 2 +...+α K X K
chiamato combinazione lineare vettori X K .
Se ci sono tali numeri diversi da zero α K ≠ 0, K = 1,..., K, che cosa y = 0 , quindi un tale insieme di vettori X K chiamato linearmente dipendente. In caso contrario, i vettori sono detti linearmente indipendenti. Ad esempio, vettori X 1 = (2, 2) t e X 2 = (−1, −1) t sono linearmente dipendenti, poiché X 1 +2X 2 = 0
Considera un set di K vettori X 1 , X 2 ,...,X K dimensioni N. Il rango di questo sistema di vettori è il numero massimo di vettori linearmente indipendenti. Ad esempio nel set
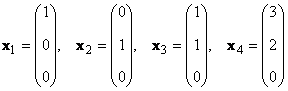
ci sono solo due vettori linearmente indipendenti, per esempio X 1 e X 2 , quindi il suo rango è 2.
Ovviamente, se nell'insieme sono presenti più vettori della loro dimensione ( K>N), allora sono necessariamente linearmente dipendenti.
Grado di matrice(indicato da rango( UN)) è il rango del sistema di vettori che lo compone. Sebbene qualsiasi matrice possa essere rappresentata in due modi (vettori di colonna o vettori di riga), ciò non influisce sul valore del rango, poiché
matrice quadrata UN si dice non degenerato se ha un unico inversione matrice UN-1 , determinato dalle condizioni
aa −1 = UN −1 UN = io.
La matrice inversa non esiste per tutte le matrici. Una condizione necessaria e sufficiente per la non degenerazione è
det( UN) ≠ 0 o rango( UN) = N.
L'inversione della matrice è una procedura complessa per la quale esistono programmi speciali. Per esempio,
Riso. 17 Inversione della matrice
Diamo formule per il caso più semplice: matrici 2 × 2
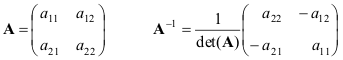
Se matrici UN e B non sono degenerati, quindi
(AB) −1 = B −1 UN −1 .
Se la matrice UNè degenerato e matrice inversa non esiste, in alcuni casi si può usare pseudo-inverso matrice, che è definita come tale matrice UN+ quello
aa + UN = UN.
La matrice pseudo-inversa non è l'unica e la sua forma dipende dal metodo di costruzione. Ad esempio, per una matrice rettangolare, puoi utilizzare il metodo Moore-Penrose.
Se il numero di colonne è inferiore al numero di righe, allora
UN + =(UN t UN) −1 UN t
Per esempio,
Riso. 17a Pseudo inversione di matrice
Se il numero di colonne più numero righe, quindi
UN + =UN t ( aa t) −1
Vettore X può essere moltiplicato per una matrice UN dimensione adeguata. In questo caso, il vettore colonna viene moltiplicato a destra Ascia e la stringa del vettore è a sinistra X t UN. Se la dimensione del vettore J, e la dimensione della matrice io× J allora il risultato è un vettore di dimensione io. Per esempio,
Riso. 18 Moltiplicazione a matrice vettoriale
Se la matrice UN- quadrato ( io× io), quindi il vettore y = Ascia ha le stesse dimensioni di X. È ovvio che
UN(α 1 X 1 + α 2 X 2) = α 1 Ascia 1 + α 2 Ascia 2 .
Pertanto le matrici possono essere considerate come trasformazioni lineari di vettori. In particolare X = X, Bue = 0 .
Permettere UN- dimensione della matrice io× J, un b- vettore di dimensione J. Considera l'equazione
Ascia = b
rispetto al vettore X, dimensioni io. In sostanza, questo è un sistema di io equazioni lineari con J sconosciuto X 1 ,...,X J. Una soluzione esiste se e solo se
rango( UN) = rango( B) = R,
dove Bè la matrice della dimensione aumentata io×( J+1) costituito dalla matrice UN, imbottito con colonna b, B = (UN b). In caso contrario, le equazioni non sono coerenti.
Se una R = io = J, allora la soluzione è unica
X = UN −1 b.
Se una R < io, poi ce ne sono molti varie soluzioni, che può essere espresso in termini di una combinazione lineare J−R vettori. Sistema di equazioni omogenee Ascia = 0 con matrice quadrata UN (N× N) ha una soluzione non banale ( X ≠ 0 ) se e solo se det( UN) = 0. Se R= rango( UN)<N, poi ci sono N−R soluzioni linearmente indipendenti.
Se una UN- questo è matrice quadrata, un X e y- vettori della dimensione corrispondente, quindi il prodotto scalare della forma X t Ay chiamato bilineare la forma definita dalla matrice UN. In X = y espressione X t Ascia chiamato quadratico modulo.
matrice quadrata UN chiamato definito positivo, se per qualsiasi vettore diverso da zero X ≠ 0 ,
X t Ascia > 0.
Il negativo (X t Ascia < 0), non negativo (X t Ascia≥ 0) e non positivo (X t Ascia≤ 0) determinate matrici.
Se la matrice simmetrica UNè definito positivo, allora c'è un'unica matrice triangolare u con elementi positivi, per cui
UN = u t u.
Per esempio,
Riso. 19 Decomposizione di Cholesky
Permettere UNè una matrice quadrata non degenerata di dimensione N× N. Poi c'è un unico polare prestazione
UN = SR,
dove Sè una matrice simmetrica non negativa, e Rè una matrice ortogonale. matrici S e R può essere definito esplicitamente:
S 2 = aa t o S = (aa t) ½ e R = S −1 UN = (aa t) −½ UN.
Per esempio,
Riso. 20 Decomposizione polare
Se la matrice UNè degenere, quindi la scomposizione non è unica, ovvero: S ancora solo, ma R potrebbero essercene molti. La decomposizione polare rappresenta una matrice UN come combinazione di compressione/allungamento S e girando R.
Permettere UNè una matrice quadrata. Vettore v chiamato proprio vettore matrici UN, Se
Av = λ v,
dove viene chiamato il numero λ autovalore matrici UN. Quindi, la trasformazione che esegue la matrice UN su vettore v, si riduce a un semplice allungamento o compressione con un fattore λ. L'autovettore è determinato fino alla moltiplicazione per la costante α ≠ 0, cioè Se vè un autovettore, allora α vè anche un autovettore.
Alla matrice UN, dimensione ( N× N) non può essere maggiore di N autovalori. Soddisfano equazione caratteristica
det( UN − λ io) = 0,
essendo equazione algebrica N-esimo ordine. In particolare, per una matrice 2×2, l'equazione caratteristica ha la forma
Per esempio,
Riso. 21 Autovalori
Insieme di autovalori λ 1 ,..., λ N matrici UN chiamato spettro UN.
Lo spettro ha diverse proprietà. In particolare
det( UN) = λ 1×...×λ N, Sp( UN) = λ 1 +...+λ N.
Gli autovalori di una matrice arbitraria possono essere numeri complessi, ma se la matrice è simmetrica ( UN t = UN), allora i suoi autovalori sono reali.
Alla matrice UN, dimensione ( N× N) non può essere maggiore di N autovettori, ognuno dei quali corrisponde al proprio valore. Per determinare l'autovettore v n devi risolvere un sistema di equazioni omogenee
(UN − λ n io)v n = 0 .
Ha una soluzione non banale perché det( UN-λ n io) = 0.
Per esempio,
Riso. 22 autovettori
Gli autovettori di una matrice simmetrica sono ortogonali.
