2π periódusú periodikus függvények Fourier sorozata.
A Fourier sorozat lehetővé teszi a periodikus függvények komponensekre bontásával történő tanulmányozását. váltakozó áramok jellemzőek a hajtókarok feszültségei, elmozdulásai, sebessége és gyorsulása, valamint az akusztikus hullámok gyakorlati példák periodikus függvények alkalmazása mérnöki számításokban.
A Fourier-sorozat bővítése azon a feltételezésen alapul, hogy minden gyakorlati érték A -π ≤x≤ π intervallum függvényei konvergens trigonometrikus sorozatként fejezhetők ki (egy sorozat akkor tekinthető konvergensnek, ha a részeiből álló részösszegek sorozata konvergál):
Szabványos (=szokásos) jelölés a sinx és cosx összegén keresztül
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
ahol a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. valós állandók, azaz.
Ahol a -π és π közötti tartományban a Fourier-sor együtthatóit a következő képletekkel számítjuk ki:
Az a o ,a n és b n együtthatókat nevezzük Fourier-együtthatók, és ha megtalálhatók, akkor az (1) sorozatot hívjuk meg Fourier közelében, az f(x) függvénynek megfelelő. Az (1) sorozatnál az (a 1 cosx+b 1 sinx) kifejezést az első ill főharmonika,
A sorozat írásának másik módja az acosx+bsinx=csin(x+α) reláció használata
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Ahol a o egy állandó, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 a különböző komponensek amplitúdói, és egyenlő a n \ u003d arctg a n /b n.
Az (1) sorozatnál az (a 1 cosx + b 1 sinx) vagy c 1 sin (x + α 1) kifejezést az első ill. főharmonika,(a 2 cos2x+b 2 sin2x) vagy c 2 sin(2x+α 2) ún. második harmonikus stb.
Egy összetett jel pontos ábrázolásához általában végtelen számú kifejezésre van szükség. Sok gyakorlati probléma esetén azonban elegendő csak az első néhány kifejezést figyelembe venni.
Nem periódusos függvények Fourier sorozata 2π periódussal.
Nem periodikus függvények dekompozíciója.
Ha az f(x) függvény nem periodikus, akkor nem bontható ki Fourier-sorba x összes értékére. Azonban lehetséges olyan Fourier-sort definiálni, amely egy függvényt reprezentál bármely 2π szélességi tartományban.
Adott egy nem periódusos függvény, akkor új függvényt állíthatunk össze, ha egy bizonyos tartományon belül kiválasztunk f(x) értékeket, és 2π intervallumonként megismételjük azokat ezen a tartományon kívül. Mivel az új függvény periodikus, 2π periódussal, ezért minden x értékre Fourier-sorba bővíthető. Például az f(x)=x függvény nem periodikus. Ha azonban a 0-tól 2π-ig terjedő intervallumban szükséges Fourier-sorozattá bővíteni, akkor ezen az intervallumon kívül egy 2π periódusú periodikus függvény készül (ahogy az alábbi ábrán látható).
Nem periodikus függvényeknél, például f(x)=x, a Fourier-sor összege az adott tartomány minden pontjában egyenlő f(x) értékkel, de pontok esetén nem egyenlő f(x) értékkel. tartományon kívül. Egy nem periodikus függvény Fourier-sorának megtalálásához a 2π tartományban a Fourier-együtthatók ugyanazt a képletét használjuk.
Páros és páratlan függvények.
Azt mondják, az y=f(x) függvény még ha f(-x)=f(x) x minden értékére. A páros függvények grafikonjai mindig szimmetrikusak az y tengelyre (azaz tükröződnek). Két példa a páros függvényekre: y=x 2 és y=cosx.
Azt mondják, hogy az y=f(x) függvény páratlan, ha f(-x)=-f(x) x minden értékére. A páratlan függvények grafikonjai mindig szimmetrikusak az origóra.
Sok függvény nem páros és nem páratlan.
Fourier-soros bővítés koszinuszokban.
A 2π periódusú f(x) páros periodikus függvény Fourier-sora csak koszinusz tagokat tartalmaz (azaz nem tartalmaz szinusztagokat), és tartalmazhat konstans tagot is. Következésképpen,
hol vannak a Fourier-sor együtthatói,
A 2π periódusú f(x) páratlan periodikus függvény Fourier-sora csak szinuszos tagokat tartalmaz (azaz nem tartalmaz koszinuszos tagokat).
Következésképpen,
hol vannak a Fourier-sor együtthatói,
Fourier-sorozat félcikluson.
Ha egy függvény egy tartományra van definiálva, mondjuk 0-tól π-ig, és nem csak 0-tól 2π-ig, akkor csak szinuszokkal vagy csak koszinuszokkal bővíthető sorozattá. Az így kapott Fourier-sort ún Fourier közelében fél cikluson.
Ha bomlást akarsz kapni Fourier félcikluson koszinuszban f(x) függvényeket a 0-tól π-ig terjedő tartományban, akkor páros periodikus függvényt kell összeállítani. ábrán. alább látható az f(x)=x függvény, amely az x=0 és x=π közötti intervallumra épül. Mivel a páros függvény szimmetrikus az f(x) tengelyre, húzzuk meg az AB egyenest, ahogy az ábra mutatja. lent. Ha feltételezzük, hogy a vizsgált intervallumon kívül a kapott háromszög alakzat periodikus 2π periódussal, akkor a végső gráfnak van formája, megjelenítése. ábrán. lent. Mivel a Fourier-kiterjesztést koszinuszokban kell megkapni, mint korábban, kiszámítjuk az a o és a n Fourier-együtthatókat.
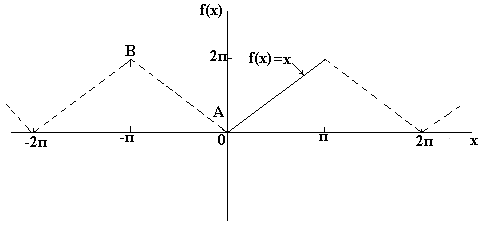
Ha meg kell szereznie szinuszos félciklusú Fourier-tágulás f(x) függvény 0-tól π-ig terjedő tartományban, akkor páratlan periodikus függvényt kell összeállítani. ábrán. alább látható az f(x)=x függvény, amely az x=0 és x=π közötti intervallumra épül. Mivel a páratlan függvény szimmetrikus az origóhoz képest, megszerkesztjük a CD vonalat, amint az ábra mutatja. Ha feltételezzük, hogy a vizsgált intervallumon kívül a vett fűrészfog jel periodikus, 2π periódussal, akkor a végső grafikon az 1. ábrán látható alakot kapja. Mivel a Fourier-tágulást félcikluson kell megkapni szinuszokban, mint korábban, a Fourier-együtthatót számítjuk ki. b
Fourier-sorok tetszőleges intervallumhoz.
Periodikus függvény bővítése L periódussal.
Az f(x) periodikus függvény ismétlődik, ha x növekszik L-vel, azaz. f(x+L)=f(x). A korábban vizsgált 2π periódusú függvényekről az L periódusú függvényekre való átmenet meglehetősen egyszerű, hiszen változó változtatással is megtehető.
Ahhoz, hogy az f(x) függvény Fourier-sorát megtaláljuk a -L/2≤x≤L/2 tartományban, bevezetünk egy új u változót úgy, hogy az f(x) függvény u-hoz képest 2π periódusú legyen. Ha u=2πx/L, akkor x=-L/2 u=-π esetén és x=L/2 u=π esetén. Legyen f(x)=f(Lu/2π)=F(u) is. Az F(u) Fourier-sor alakja a következő
(Az integrációs határértékeket bármely L hosszúságú intervallum helyettesítheti, például 0-tól L-ig)
Fourier-sor félcikluson az L≠2π intervallumban megadott függvényekhez.
Az u=πx/L helyettesítésnél az x=0 és x=L közötti intervallum az u=0 és u=π közötti intervallumnak felel meg. Ezért a függvény csak koszinuszban vagy csak szinuszban bontható ki sorozattá, azaz. ban ben Fourier sorozat fél cikluson.
A 0-tól L-ig terjedő tartományban a koszinuszokban a bővítés alakja
Amik már nagyon elege vannak. És úgy érzem, eljött az a pillanat, amikor az elmélet stratégiai tartalékaiból új konzerveket kell kinyerni. Lehetséges más módon a függvényt sorozattá bővíteni? Például egy egyenes szakaszt szinuszokkal és koszinuszokkal kifejezni? Hihetetlennek tűnik, de ezek a látszólag távoli funkciók alkalmasak rá
"újraegyesülés". Az ismert elméleti és gyakorlati fokozatokon kívül más megközelítések is léteznek a függvény sorozattá bővítésére.
Ebben a leckében megismerkedünk a trigonometrikus Fourier-sorral, érintjük konvergenciájának és összegének kérdését, és természetesen számos példát elemezünk a függvények Fourier-sorokká bővítésére. Őszintén szerettem volna a cikket „Fourier Series for Dummies”-nek nevezni, de ez ravaszság lenne, mivel a problémák megoldásához a matematikai elemzés más szakaszainak ismeretére és némi gyakorlati tapasztalatra van szükség. Ezért a preambulum az űrhajósok képzésére fog hasonlítani =)
Először is, az oldal anyagainak tanulmányozását kiváló formában kell megközelíteni. Álmos, kipihent és józan. A törött hörcsögláb miatti erős érzelmek és az élet nehézségeiről szóló rögeszmés gondolatok nélkül akváriumi halak. A Fourier-sorozat megértése szempontjából nem nehéz, a gyakorlati feladatok azonban egyszerűen megkívánják fokozott koncentráció figyelem - ideális esetben teljesen el kell hagynia a külső ingereket. A helyzetet súlyosbítja, hogy nincs egyszerű módja a megoldás és a válasz ellenőrzésének. Így, ha egészségi állapota átlag alatti, akkor jobb, ha valami egyszerűbbet csinál. Igazság.
Másodszor, mielőtt az űrbe repülne, tanulmányoznia kell a műszerfalat űrhajó. Kezdjük azoknak a függvényeknek az értékeivel, amelyekre rá kell kattintani a gépen:
Bármilyen természeti értékhez:
egy) . Valójában a szinuszos "villog" az x tengelyen minden "pi"-n keresztül:
. Az argumentum negatív értékei esetén az eredmény természetesen ugyanaz lesz: .
2). De ezt nem mindenki tudta. A "pi en" koszinusz a "villogó fény" megfelelője:
Egy negatív érv nem változtat az eseten: 
.
Talán elég.
És harmadszor, kedves űrhajós alakulat, képesnek kell lennie arra, hogy ... egyesít.
Főleg persze függvényt hozzon differenciáljel alá, részenként integrálniés jó viszonyban lenni vele Newton-Leibniz képlet. Kezdjük a fontos repülés előtti gyakorlatokkal. Erősen nem ajánlom kihagyását, nehogy később nulla gravitációban ellaposodjon:
1. példa
Határozott integrálok kiszámítása
ahol természeti értékeket vesz.
Megoldás: az integráció az "x" változón keresztül történik, és ebben a szakaszban az "en" diszkrét változót állandónak tekintjük. Minden integrálban vigye a függvényt a differenciál jele alá:
A megoldás rövid változata, amelyre jó lenne lőni, így néz ki:
Hozzászokni:
A fennmaradó négy pont önmaga. Igyekezzen lelkiismeretesen kezelni a feladatot, és az integrálokat röviden rendezni. Az óra végén mintamegoldások.
MINŐSÉGI gyakorlat után szkafandert vettünk fel
és készülj a kezdésre!
Tekintsünk egy olyan függvényt meghatározott legalábbis az intervallumon (és esetleg nagyobb intervallumon). Ha ez a függvény integrálható a szegmensbe, akkor trigonometrikussá bővíthető Fourier sorozat:
, hol vannak az ún Fourier-együtthatók.
Ebben az esetben hívják a számot bomlási időszak, és a szám az felezési idejű bomlás.
Nyilvánvaló, hogy általános esetben a Fourier-sor szinuszokból és koszinuszokból áll: 
Valóban, írjuk le részletesen:
A sorozat nulla tagját általában így írják.
A Fourier-együtthatókat a következő képletekkel számítjuk ki: 
Tökéletesen megértem, hogy az új kifejezések még mindig homályosak a téma tanulmányozására kezdők számára: bomlási időszak, fél ciklus, Fourier-együtthatókés mások. Ne essen pánikba, ez nem hasonlítható össze az űrséta előtti izgalommal. Találjunk ki mindent a legközelebbi példában, amelynek végrehajtása előtt logikus, hogy sürgető gyakorlati kérdéseket teszünk fel:
Bontsa ki a függvényt Fourier-sorba. Ezenkívül gyakran meg kell rajzolni egy függvény grafikonját, egy sorozat összegének grafikonját, egy részösszeget, és kifinomult professzori fantáziák esetén valami mást kell tenni.
Lényegében meg kell találni Fourier-együtthatók, azaz hármat állítson össze és számoljon ki határozott integrálok.
Kérjük, másolja be a füzetébe a Fourier-sorozat általános formáját és a három munkaképletet. Nagyon örülök, hogy az oldal látogatói közül néhányan a szemem láttára valósul meg gyerekkori álma, hogy űrhajós legyen =)
2. példa
Bontsa ki a függvényt egy Fourier-sorozattá az intervallumon. Készítsen grafikont, egy sorozat összegének és egy részösszegének grafikonját.
Megoldás: a feladat első része a függvény kiterjesztése Fourier-sorba.
Az eleje szabványos, feltétlenül írja le, hogy:
Ebben a problémában a terjeszkedési időszak , félidőszak .
Kibővítjük a függvényt egy Fourier-sorral az intervallumon: 
A megfelelő képletek segítségével megtaláljuk Fourier-együtthatók. Most hármat kell összeállítanunk és kiszámolnunk határozott integrálok. A kényelem kedvéért számozom a pontokat:
1) Az első integrál a legegyszerűbb, de ehhez már kell egy szem és egy szem: 
2) A második képletet használjuk:
Ez az integrál jól ismert és darabonként veszi: 
Amikor használtan találták egy függvény differenciáljel alá hozásának módszere.
A vizsgált feladatban kényelmesebb azonnal használni egy meghatározott integrálban lévő részek szerinti integrálási képlet 
:
Egy-két technikai megjegyzés. Először is a képlet alkalmazása után a teljes kifejezést nagy zárójelek közé kell tenni, mivel az eredeti integrál előtt van egy konstans. Ne veszítsük el! A zárójelek bármelyik további lépésnél nyithatók, én a legutolsó kanyarnál tettem. Az első "darabban" 
rendkívüli pontosságot mutatunk a helyettesítésben, amint látható, a konstans nem működik, és az integráció határai behelyettesítésre kerülnek a termékbe. Ezt a műveletet szögletes zárójelek jelölik. Nos, a képlet második "darabjának" integrálját jól ismered az edzésfeladatból ;-)
És ami a legfontosabb - a figyelem végső koncentrációja!
3) Keressük a harmadik Fourier-együtthatót:
Az előző integrál rokonát kapjuk, ami szintén alkatrészekkel integrálva:
Ez a példa egy kicsit bonyolultabb, lépésről lépésre leírom a további lépéseket: 
(1) A teljes kifejezés nagy zárójelben van.. Nem akartam unalmasnak tűnni, túl gyakran veszítik el az állandót.
(2) B ez az eset Azonnal kinyitottam azokat a nagy zárójeleket. Speciális figyelem
az első „darabnak” szenteljük: az állandó füstölgés a pálya szélén, és nem vesz részt a termékbe való integráció határainak (és ) helyettesítésében. Tekintettel a rekord zűrzavarára, ezt a műveletet ismét ajánlatos szögletes zárójelben kiemelni. A második "darabbal" 
minden egyszerűbb: itt a tört nagy zárójelek megnyitása után jelent meg, a konstans pedig - az ismerős integrál integrálása eredményeként ;-)
(3) Szögletes zárójelben transzformációt végzünk, a jobb oldali integrálban pedig behelyettesítjük az integrálás határait.
(4) A szögletes zárójelekből kivesszük a „villogót”: , ezután kinyitjuk a belső zárójeleket: .
(5) A zárójelben szereplő 1-et és -1-et töröljük, végső egyszerűsítéseket végzünk.
Végül megtalálta mindhárom Fourier-együtthatót: 
Helyettesítsd be őket a képletbe 
:
Ne felejtsd el kettéosztani. Az utolsó lépésben a konstans ("mínusz kettő"), amely nem függ az "en"-től, kikerül az összegből.
Így megkaptuk a függvény kiterjesztését egy Fourier-sorban a következő intervallumon: 
Vizsgáljuk meg a Fourier-sorok konvergenciájának kérdését. Külön kifejtem az elméletet Dirichlet-tétel, szó szerint "az ujjakon", tehát ha szigorú megfogalmazásokra van szüksége, kérjük, olvassa el a kalkulus tankönyvet (például Bohan 2. kötete; vagy Fichtenholtz 3. kötete, de abban nehezebb).
A feladat második részében grafikont, sorozatösszeggráfot és részösszeggráfot kell rajzolni.
A függvény grafikonja a szokásos egyenes vonal a síkon, amely fekete pontozott vonallal van megrajzolva: 
A sorozat összegével foglalkozunk. Mint tudják, a funkcionális sorozatok függvényekhez konvergálnak. Esetünkben a felépített Fourier-sor 
"x" tetszőleges értékére a pirossal jelzett függvényhez konvergál. Ez a funkció elviseli 1. típusú szünetek pontokban , hanem bennük is definiálva (piros pontok a rajzon)
Ilyen módon: 
. Könnyen belátható, hogy jelentősen eltér az eredeti függvénytől, ezért a jelölésben 
egyenlőségjel helyett tildát használnak.
Vizsgáljuk meg azt az algoritmust, amellyel kényelmesen meg lehet alkotni egy sorozat összegét.
A központi intervallumon a Fourier-sor magához a függvényhez konvergál (a központi piros szegmens egybeesik a lineáris függvény fekete pontozott vonalával).
Most beszéljünk egy kicsit a figyelembe vett trigonometrikus bővítés természetéről. Fourier sorozat 
csak periodikus függvényeket tartalmaz (konstans, szinusz és koszinusz), tehát a sorozat összege 
szintén periodikus függvény.
Mit jelent ez nálunk konkrét példa? Ez pedig azt jelenti, hogy a sorozat összege 
–szükségszerűen időszakos az intervallum piros szakaszát pedig végtelenül meg kell ismételni a bal és a jobb oldalon.
Azt hiszem, most végre világossá vált a "bomlási időszak" kifejezés jelentése. Egyszerűen fogalmazva, minden alkalommal, amikor a helyzet újra és újra megismétlődik.
A gyakorlatban általában elegendő három dekompozíciós periódus ábrázolása, ahogy az a rajzon is történik. Nos, és még több "csonk" a szomszédos időszakokról - hogy egyértelmű legyen, hogy a diagram folytatódik.
Különösen érdekesek 1. típusú folytonossági pontok. Ilyen pontokon a Fourier-sor izolált értékekhez konvergál, amelyek pontosan a folytonossági "ugrás" közepén helyezkednek el (piros pontok a rajzon). Hogyan lehet megtalálni ezeknek a pontoknak az ordinátáját? Először keressük meg a "felső emelet" ordinátáját: ehhez kiszámítjuk a függvény értékét a központi bővítési periódus jobb szélső pontjában: . Az „alsó emelet” ordinátájának kiszámításához a legegyszerűbb módja annak, hogy ugyanazon periódus bal szélső értékét vegyük: 
. Az átlagérték ordinátája a "felső és alsó" összegének számtani közepe: . Jó az a tény, hogy a rajz elkészítésekor azonnal látni fogod, hogy a közepe jól vagy rosszul van-e kiszámolva.
Szerkesszük meg a sorozat részösszegét, és egyúttal ismételjük meg a „konvergencia” kifejezés jelentését. Az indíték a kb. leckéből ismert a számsor összege. Ismertesse részletesen gazdagságunkat:
Részösszeg elkészítéséhez a sorozat nullát + további két tagját kell felírni. vagyis
A rajzon a függvény grafikonja zölden látható, és mint látható, elég szorosan körbeveszi a teljes összeget. Ha a sorozat öt tagjának részösszegét vesszük figyelembe, akkor ennek a függvénynek a grafikonja még pontosabban közelíti a piros vonalakat, ha száz tag van, akkor a „zöld kígyó” valójában teljesen összeolvad a piros szegmensekkel, stb. Így a Fourier-sor konvergál az összegéhez.
Érdekes megjegyezni, hogy bármely részösszeg folyamatos funkció, de a sorozat teljes összege még mindig nem folyamatos.
A gyakorlatban nem ritka a részösszeg gráf felépítése. Hogyan kell csinálni? Esetünkben figyelembe kell venni a szegmens függvényét, kiszámítani az értékeit a szegmens végén és a közbenső pontokon (minél több pontot vesz figyelembe, annál pontosabb lesz a grafikon). Ezután jelölje meg ezeket a pontokat a rajzon, és óvatosan rajzoljon egy grafikont a periódusra, majd „másolja” azt szomszédos intervallumokra. Hogyan másképp? Hiszen a közelítés is periodikus függvény ... ... a grafikonja valahogy egy orvosi eszköz kijelzőjén egyenletes szívritmusra emlékeztet.
Természetesen nem túl kényelmes az építkezés, mivel rendkívül óvatosnak kell lennie, legalább fél milliméteres pontossággal. A rajzolással ellentmondó olvasóknak azonban örömet okozok - egy "igazi" feladatnál messze nem mindig kell rajzolni, valahol az esetek 50%-ában szükséges a funkciót Fourier-sorossá bővíteni, és ez az azt.
A rajz elkészítése után teljesítjük a feladatot:
Válasz: 
Sok feladatnál a funkció szenved 1. típusú szakadás közvetlenül a bomlási perióduson:
3. példa
Bontsa ki egy Fourier-sorozatban az intervallumon megadott függvényt. Rajzolja fel a függvény és a sorozatok összegének grafikonját!
A javasolt függvény darabonként van megadva (és ne feledje, csak a szegmensben)és elviselni 1. típusú szakadás pontban. Ki lehet számítani a Fourier-együtthatókat? Nincs mit. A függvény bal és jobb része is integrálható a saját intervallumán, ezért a három képletben szereplő integrálokat két integrál összegeként kell ábrázolni. Nézzük meg például, hogyan történik ez nulla együttható esetén:
A második integrál nullának bizonyult, ami csökkentette a munkát, de ez nem mindig van így.
Két másik Fourier-együttható is hasonlóan van felírva.
Hogyan lehet megjeleníteni egy sorozat összegét? A bal oldali intervallumon egy egyenes szakaszt rajzolunk, az intervallumon pedig egy egyenes szakaszt (a tengelyszakaszt jelölje ki félkövérrel). Azaz a bővítési intervallumon a sorozat összege három "rossz" pont kivételével mindenhol egybeesik a függvénnyel. A függvény diszkontinuitási pontján a Fourier-sor egy izolált értékhez konvergál, amely pontosan a diszkontinuitás „ugrásának” közepén helyezkedik el. Nem nehéz szóban látni: bal oldali határ:, jobb oldali határ: 
és nyilvánvalóan a felezőpont ordinátája 0,5.
Az összeg periodicitása miatt a képet szomszédos periódusokra kell „szorozni”, különösen, ugyanazt ábrázolni a és intervallumokon. Ebben az esetben a pontokban a Fourier-sor a medián értékekhez konvergál.
Valójában nincs itt semmi új.
Próbálja meg egyedül megoldani ezt a problémát. Hozzávetőleges minta finom tervezésről és rajzról a lecke végén.
Egy tetszőleges kiterjesztési periódus esetén, ahol az "el" bármely pozitív szám, a Fourier-sor és a Fourier-együttható képlete egy kicsit bonyolultabb szinusz- és koszinusz argumentumban különbözik:
Ha , akkor megkapjuk annak az intervallumnak a képleteit, amellyel indultunk.
A probléma megoldásának algoritmusa és elvei teljesen megmaradnak, de a számítások technikai összetettsége nő:
4. példa
Bontsa ki a függvényt Fourier-sorba, és ábrázolja az összeget. 
Megoldás: valójában a 3. példa analógja 1. típusú szakadás pontban. Ebben a problémában a terjeszkedési időszak , félidőszak . A függvény csak a fél intervallumon van definiálva, de ez nem változtat a dolgokon - fontos, hogy a függvény mindkét része integrálható legyen.
Bővítsük ki a függvényt Fourier-sorba:
Mivel a függvény nem folytonos az origóban, minden Fourier-együtthatót nyilvánvalóan két integrál összegeként kell felírni:
1) Leírom az első integrált a lehető legrészletesebben:
2) Óvatosan nézzen bele a Hold felszínébe:
Második integrál részekre szedni:
Mire kell nagyon odafigyelni, miután a megoldás folytatását csillaggal nyitjuk?
Először is, nem veszítjük el az első integrált 
, ahol azonnal végrehajtjuk a differenciálmű jele alá hozva. Másodszor, ne felejtsd el a balszerencsés állandót a nagy zárójelek előtt és ne keveredjen össze a jelek a képlet használatakor 
. A nagy konzolokat végül is kényelmesebb azonnal kinyitni a következő lépésben.
A többi már technika kérdése, csak az integrálok megoldásában való elégtelen tapasztalat okozhat nehézséget.
Igen, nem hiába háborodtak fel a francia matematikus Fourier jeles kollégái - hogyan merte a függvényeket trigonometrikus sorozatokra bontani?! =) Egyébként valószínűleg mindenkit érdekel a szóban forgó feladat gyakorlati jelentése. Fourier maga is dolgozott matematikai modell hővezető képességét, majd később a róla elnevezett sorozatot számos periodikus folyamat vizsgálatára kezdték használni, amelyek látszólag láthatatlanok a környező világban. Most egyébként azon kaptam magam, hogy nem véletlenül hasonlítottam össze a második példa grafikonját egy periodikus szívritmussal. Aki szeretne, megismerkedhet praktikus alkalmazás Fourier transzformációk harmadik fél forrásaiból. ... Bár jobb, ha nem – első szerelemként emlékeznek rá =)
3) Tekintettel a többször említett gyenge láncszemekre, a harmadik együtthatóval foglalkozunk:
Integrálás részenként: 
A talált Fourier-együtthatókat behelyettesítjük a képletbe 
, ne felejtsük el kettéosztani a nulla együtthatót:
Ábrázoljuk a sorozat összegét. Röviden ismételjük meg az eljárást: az intervallumra építünk egy sort, az intervallumra pedig egy sort. Az "x" nulla értékével egy pontot teszünk a rés "ugrásának" közepére, és "megismételjük" a diagramot a szomszédos időszakokra: 
A periódusok "csomópontjain" az összeg egyenlő lesz a rés "ugrásának" felezőpontjaival is.
Kész. Emlékeztetlek arra, hogy maga a függvény feltételesen csak a félintervallumon van definiálva, és nyilvánvalóan egybeesik az intervallumokon lévő sorozatok összegével
Válasz:
Néha egy darabonként adott függvény is folyamatos a bővítési perióduson. A legegyszerűbb példa: 
. Megoldás (Lásd Bohan 2. kötet) ugyanaz, mint az előző két példában: annak ellenére funkció folytonossága pontban minden Fourier-együttható két integrál összegeként van kifejezve.
A szakítási intervallumban 1. típusú folytonossági pontokés/vagy a grafikon "csomópontja" több is lehet (kettő, három és általában bármelyik végsőösszeg). Ha egy függvény minden alkatrészre integrálható, akkor Fourier sorozatban is bővíthető. De gyakorlati tapasztalatból nem emlékszem ilyen bádogra. Mindazonáltal vannak bonyolultabb feladatok is, mint amit csak gondoltunk, és a cikk végén mindenki számára elérhetők a megnövekedett összetettségű Fourier-sorozatra mutató hivatkozások.
Addig is lazítsunk, dőljünk hátra székünkben, és elmélkedjünk a csillagok végtelen kiterjedésén:
5. példa
Bontsa ki a függvényt Fourier-sorrá az intervallumon, és ábrázolja a sorozat összegét.
Ebben a feladatban a függvény folyamatos a bontási félintervallumon, ami leegyszerűsíti a megoldást. Minden nagyon hasonló a 2. példához. Az űrhajó elől nem szabadulhatsz meg - dönteni kell =) Tervezési minta az óra végén, az órarend mellékelve.
Páros és páratlan függvényekkel a probléma megoldásának folyamata észrevehetően leegyszerűsödik. És ezért. Térjünk vissza a függvény kiterjesztéséhez egy Fourier-sorban "két pi" perióduson. 
és tetszőleges időszak "két sör" 
.
Tegyük fel, hogy a függvényünk páros. A sorozat általános kifejezése, mint látható, páros koszinuszokat és páratlan szinuszokat tartalmaz. És ha felbontunk egy PÁROS függvényt, akkor miért kellenek páratlan szinuszok?! Állítsuk vissza a szükségtelen együtthatót: .
Ily módon egy páros függvény csak koszinuszokban bővül Fourier-sorrá:
Mert a páros függvények integráljai A nullához képest szimmetrikus integrációs szegmens felett megduplázható, akkor a Fourier-együttható többi része is egyszerűsödik.
Terjedelemhez: 
Tetszőleges intervallumhoz: 
A tankönyvpéldák, amelyek szinte minden számítástechnikai tankönyvben megtalálhatók, tartalmazzák a páros függvények kiterjesztését 
. Ezenkívül személyes praxisomban többször is találkoztak:
6. példa
Adott egy függvény. Kívánt:
1) bontsa ki a függvényt egy Fourier-sorba a ponttal, ahol egy tetszőleges pozitív szám;
2) írja fel az intervallum bővítését, építsen fel egy függvényt, és ábrázolja a sorozat teljes összegét.
Megoldás: az első bekezdésben javasolt a probléma megoldása ben Általános nézetés nagyon kényelmes! Szükség lesz – csak helyettesítse az értékét.
1) Ebben a feladatban a terjeszkedési periódus , félidőszak . A további cselekvések során, különösen az integráció során, az "el" állandónak számít
A függvény páros, ami azt jelenti, hogy csak koszinuszokban bővül Fourier-sorrá: 
.
Fourier-együtthatókat keresünk a képletekkel 
. Ügyeljen abszolút előnyeikre. Először is az integrációt a bővítés pozitív szegmensén hajtjuk végre, ami azt jelenti, hogy biztonságosan megszabadulunk a modultól 
, figyelembe véve csak az "x"-et két darabból. Másodszor pedig az integráció észrevehetően leegyszerűsödik.
Két: 
Integrálás részenként:
Ilyen módon:
, míg a konstans, amely nem függ az "en"-től, kikerül az összegből.
Válasz: 
2) Az intervallumra írjuk a bővítést, ehhez behelyettesítjük a félperiódus kívánt értékét az általános képletbe:
A 2p periódusú f(x) páros periodikus függvény Fourier-sora csak koszinusz tagokat tartalmaz (azaz nem tartalmaz szinusztagokat), és tartalmazhat konstans tagot is. Következésképpen,
hol vannak a Fourier-sor együtthatói,
A 2p periódusú f (x) páratlan periodikus függvény Fourier-sora csak szinuszos tagokat tartalmaz (azaz nem koszinuszos tagokat).
Következésképpen,
hol vannak a Fourier-sor együtthatói,
Ha egy függvény egy tartományra van definiálva, mondjuk 0-tól p-ig, és nem csak 0-tól 2p-ig, akkor csak szinuszokkal vagy csak koszinuszokkal bővíthető sorozattá. Az így kapott Fourier-sort ún mellett Fourier a fél ciklus.
Ha bomlást akarsz kapni Fourier a fél ciklus tovább koszinuszokat f (x) függvények 0-tól p-ig terjedő tartományban, akkor páros periodikus függvényt kell összeállítani. ábrán. alább látható az f (x) =x függvény, amely az x=0 és x=p közötti intervallumra épül. Mivel a páros függvény szimmetrikus az f (x) tengelyre, húzzuk meg az AB egyenest, ahogy az ábra mutatja. lent. Ha feltételezzük, hogy a vizsgált intervallumon kívül a kapott háromszög alakzat periodikus 2p periódussal, akkor a végső gráfnak van formája, megjelenítése. ábrán. lent. Mivel a Fourier-kiterjesztést koszinuszokban kell megkapni, mint korábban, kiszámítjuk az a o és a n Fourier-együtthatókat.
Ha meg kell szereznie bomlás Fourier a fél ciklus tovább melléküregek f (x) függvény 0 és p tartományban van, akkor páratlan periodikus függvényt kell összeállítani. ábrán. alább látható az f(x)=x függvény, amely az x=0 és x=p közötti intervallumra épül. Mivel a páratlan függvény szimmetrikus az origóhoz képest, megszerkesztjük a CD vonalat, amint az ábra mutatja.
Ha feltételezzük, hogy a vizsgált intervallumon kívül a vett fűrészfog jel periodikus, 2p periódussal, akkor a végső grafikon az 1. ábrán látható alakot kapja. Mivel a Fourier-tágulást félcikluson kell megkapni szinuszokban, mint korábban, a Fourier-együtthatót számítjuk ki. b
Hogyan lehet matematikai képleteket beilleszteni a webhelyre?
Ha valaha egy vagy két matematikai képletet kell hozzáadnia egy weboldalhoz, akkor ezt a legegyszerűbben a cikkben leírtak szerint teheti meg: a matematikai képletek könnyen beilleszthetők az oldalra képek formájában, amelyeket Wolfram Alpha automatikusan generál. Az egyszerűség mellett ez az univerzális módszer segít javítani a webhely láthatóságát kereső motorok. Régóta működik (és szerintem örökké működni fog), de erkölcsileg elavult.
Ha folyamatosan matematikai képleteket használ a webhelyén, akkor azt javaslom, hogy használja a MathJax-ot, egy speciális JavaScript-könyvtárat, amely MathML, LaTeX vagy ASCIIMathML jelölést használó webböngészőkben jeleníti meg a matematikai jelöléseket.
A MathJax használatának két módja van: (1) egy egyszerű kód segítségével gyorsan csatlakoztathat egy MathJax szkriptet a webhelyéhez, amely a megfelelő időben automatikusan betöltődik egy távoli szerverről (szerverek listája); (2) töltse fel a MathJax szkriptet egy távoli szerverről a szerverére, és csatlakoztassa webhelye összes oldalához. A második módszer bonyolultabb és időigényesebb, és lehetővé teszi, hogy felgyorsítsa webhelye oldalainak betöltését, és ha a szülő MathJax szerver valamilyen okból átmenetileg elérhetetlenné válik, az semmilyen módon nem érinti a saját webhelyét. Ezen előnyök ellenére az első módszert választottam, mivel az egyszerűbb, gyorsabb és nem igényel technikai ismereteket. Kövesse a példámat, és 5 percen belül használhatja a MathJax összes funkcióját a webhelyén.
A MathJax könyvtár szkriptjét távoli szerverről csatlakoztathatja a MathJax fő webhelyéről vagy a dokumentációs oldalról származó két kódopció használatával:
Ezen kódopciók egyikét ki kell másolni és be kell illeszteni a weboldal kódjába, lehetőleg a címkék közé
és vagy közvetlenül a címke után . Az első opció szerint a MathJax gyorsabban tölt be és kevésbé lassítja az oldalt. De a második lehetőség automatikusan követi és betölti a MathJax legújabb verzióit. Ha beírja az első kódot, akkor azt rendszeresen frissíteni kell. Ha beilleszti a második kódot, akkor az oldalak lassabban töltődnek be, de nem kell folyamatosan figyelnie a MathJax frissítéseit.A MathJax csatlakoztatásának legegyszerűbb módja a Blogger vagy a WordPress: a webhely vezérlőpultján adjon hozzá egy widgetet, amely harmadik fél JavaScript kódjának beillesztésére szolgál, másolja bele a fenti betöltési kód első vagy második verzióját, és helyezze közelebb a widgetet a a sablon eleje (egyébként ez egyáltalán nem szükséges, mivel a MathJax szkript aszinkron módon töltődik be). Ez minden. Most tanulja meg a MathML, LaTeX és ASCIIMathML jelölési szintaxisát, és máris beágyazhat matematikai képleteket weboldalaiba.
Bármely fraktál egy bizonyos szabály szerint épül fel, amelyet következetesen korlátlan számú alkalommal alkalmaznak. Minden ilyen időt iterációnak nevezünk.
A Menger-szivacs elkészítésének iteratív algoritmusa meglehetősen egyszerű: az 1-es oldalú eredeti kockát a lapjaival párhuzamos síkok 27 egyenlő kockára osztják. Egy központi kockát és a lapok mentén szomszédos 6 kockát eltávolítanak róla. Kiderült, hogy egy készlet 20 megmaradt kisebb kockából áll. Minden egyes kockával ugyanezt megtéve egy 400 kisebb kockából álló készletet kapunk. Ezt a folyamatot a végtelenségig folytatva megkapjuk a Menger szivacsot.
A Fourier-sor egy tetszőlegesen felvett függvény egy adott periódussal sorozatként való ábrázolása. Általánosságban ezt a megoldást egy elem ortogonális alapon történő felbontásának nevezzük. A függvények kiterjesztése a Fourier-sorokban meglehetősen hatékony eszköz különféle problémák megoldására, ennek a transzformációnak a tulajdonságai miatt az argumentumban és a konvolúcióban az integrálás, a differenciálás, valamint a kifejezés eltolása során.
Egy személy, akit nem ismer felsőbb matematika, valamint a francia tudós Fourier munkáival valószínűleg nem fogja megérteni, mik ezek a „sorozatok”, és mire valók. Közben ez az átalakulás elég sűrűvé vált az életünkben. Nemcsak matematikusok használják, hanem fizikusok, vegyészek, orvosok, csillagászok, szeizmológusok, oceanográfusok és még sokan mások. Nézzük meg közelebbről a nagy francia tudós munkáit is, aki korát megelőzve tett felfedezést.
A Fourier-sor az egyik módszer (az elemzéssel és másokkal együtt) Ez a folyamat minden alkalommal megtörténik, amikor egy személy bármilyen hangot hall. A fülünk automatikusan átalakul elemi részecskék rugalmas közegben sorokra bontják (a spektrum mentén) a hangerőszint egymást követő értékeit a különböző magasságú hangokhoz. Ezután az agy ezeket az adatokat számunkra ismerős hangokká alakítja. Mindez a vágyunk vagy tudatunk mellett, magától is megtörténik, de ahhoz, hogy megértsük ezeket a folyamatokat, több évbe telik a felsőbb matematika tanulmányozása.
A Fourier-transzformáció végrehajtható analitikai, numerikus és egyéb módszerekkel. A Fourier-sorok az oszcillációs folyamatok lebontásának számszerű módjára utalnak - az óceán árapályától és fényhullámaitól a szoláris (és más csillagászati objektumok) tevékenységi ciklusáig. Ezekkel a matematikai technikákkal lehetőség nyílik olyan függvények elemzésére, amelyek bármilyen oszcillációs folyamatot szinuszos komponensek sorozataként ábrázolnak, amelyek a minimumtól a maximumig haladnak, és fordítva. A Fourier-transzformáció egy olyan függvény, amely leírja az adott frekvenciának megfelelő szinuszok fázisát és amplitúdóját. Ezzel az eljárással nagyon összetett egyenletek oldhatók meg, amelyek hő-, fény- vagy elektromos energia hatására fellépő dinamikus folyamatokat írnak le. Ezenkívül a Fourier-sorok lehetővé teszik az állandó komponensek elkülönítését komplex oszcillációs jelekben, ami lehetővé tette a kapott kísérleti megfigyelések helyes értelmezését az orvostudományban, a kémiában és a csillagászatban.
Ennek az elméletnek az alapító atyja Jean Baptiste Joseph Fourier francia matematikus. Ezt az átalakulást később róla nevezték el. Kezdetben a tudós módszerét a hővezetés – a hő terjedésének – mechanizmusának tanulmányozására és magyarázatára alkalmazta szilárd anyagok. Fourier azt javasolta, hogy az eredeti szabálytalan eloszlás a legegyszerűbb szinuszokra bontható, amelyek mindegyikének megvan a saját hőmérsékleti minimuma és maximuma, valamint saját fázisa. Ebben az esetben minden ilyen komponenst a minimumtól a maximumig mérünk, és fordítva. A görbe felső és alsó csúcsát, valamint az egyes harmonikusok fázisait leíró matematikai függvényt a hőmérséklet-eloszlás kifejezés Fourier-transzformációjának nevezzük. Az elmélet szerzője a matematikailag nehezen leírható általános eloszlásfüggvényt egy nagyon kényelmes koszinusz és szinusz sorozatra redukálta, amelyek összegzése adja az eredeti eloszlást.
A tudós kortársai – a tizenkilencedik század elejének vezető matematikusai – nem fogadták el ezt az elméletet. A fő kifogás Fourier azon állítása volt, miszerint az egyenest vagy a nem folytonos görbét leíró nem folytonos függvény folyamatos szinuszos kifejezések összegeként ábrázolható. Példaként tekintsük Heaviside „lépését”: értéke nulla a réstől balra, és egy jobbra. Ez a függvény az elektromos áram időváltozótól való függését írja le, amikor az áramkör zárt. Az elmélet kortársai akkor még soha nem találkoztak hasonló helyzet, amikor a nem folytonos kifejezést folytonos, hagyományos függvények, például exponenciális, szinuszos, lineáris vagy másodfokú függvények kombinációjával írnák le.
Hiszen ha a matematikusnak igaza volt az állításaiban, akkor a végtelen trigonometrikus Fourier-sor összegzésével a lépésenkénti kifejezés pontos reprezentációját kaphatjuk akkor is, ha sok hasonló lépése van. A tizenkilencedik század elején egy ilyen kijelentés abszurdnak tűnt. De minden kétség ellenére sok matematikus kiterjesztette ennek a jelenségnek a vizsgálati körét, túlmutatva a hővezető képesség tanulmányozásán. A legtöbb tudóst azonban továbbra is gyötörte a kérdés: „Konvergálhat-e egy szinuszos sorozat összege pontos érték nem folyamatos funkció?"
A konvergencia kérdése akkor vetődik fel, amikor végtelen számsorokat kell összeadni. A jelenség megértéséhez vegyünk egy klasszikus példát. Elérheti-e valaha a falat, ha minden egymást követő lépés feleakkora, mint az előző? Tegyük fel, hogy két méterrel a céltól, az első lépés közelebb visz a feléhez, a következő a háromnegyedhez, és az ötödik lépés után az út közel 97 százalékát megteszed. Azonban akárhány lépést tesz meg, a szigorú matematikai értelemben vett célt nem fogja elérni. Numerikus számításokkal kimutatható, hogy végül egy tetszőlegesen kis adott távolságot is meg lehet közelíteni. Ez a bizonyítás egyenértékű annak bizonyításával, hogy a fele, egynegyede stb. összértéke egyhez fog fordulni.
újra ez a kérdés század végén emelkedett, amikor a Fourier-sorokat próbálták felhasználni az apály és áramlás intenzitásának előrejelzésére. Ebben az időben Lord Kelvin feltalált egy eszközt, amely egy analóg számítástechnikai eszköz, amely lehetővé tette a katonai és kereskedelmi flotta tengerészei számára ennek nyomon követését. természeti jelenség. Ez a mechanizmus meghatározta a fázisok és amplitúdók halmazait az árapály magasságát és a hozzájuk tartozó időpillanatokat tartalmazó táblázatból, amelyet az év során egy adott kikötőben gondosan mértek. Mindegyik paraméter a dagálymagasság-kifejezés szinuszos komponense volt, és a szabályos komponensek közé tartozott. A mérések eredményeit bevitték Lord Kelvin számológépébe, amely szintetizált egy görbét, amely a következő évre előrejelezte a víz magasságát az idő függvényében. Nagyon hamar hasonló görbék készültek a világ összes kikötőjére.
Abban az időben nyilvánvalónak tűnt, hogy egy szökőár előrejelzővel nagy mennyiség a számla elemei ki tudják számítani nagyszámú fázisokat és amplitúdókat, és így pontosabb előrejelzéseket adnak. Mindazonáltal kiderült, hogy ez a szabályszerűség nem figyelhető meg azokban az esetekben, amikor a szintetizálandó árapály-kifejezés éles ugrást tartalmazott, azaz nem folytonos volt. Abban az esetben, ha az időpillanat-táblázatból adat kerül be a készülékbe, akkor több Fourier-együtthatót számít ki. Az eredeti funkció visszaáll a szinuszos komponenseknek köszönhetően (a talált együtthatók szerint). Az eredeti és a visszaállított kifejezés közötti eltérés bármely ponton mérhető. Ismételt számítások és összehasonlítások elvégzésekor látható, hogy a legnagyobb hiba értéke nem csökken. Mindazonáltal a folytonossági pontnak megfelelő régióban lokalizálódnak, és bármely más ponton nullára hajlamosak. 1899-ben ezt az eredményt elméletileg megerősítette Joshua Willard Gibbs, a Yale Egyetem munkatársa.
A Fourier-analízis nem alkalmazható olyan kifejezésekre, amelyek egy bizonyos intervallumon belül végtelen számú burstot tartalmaznak. Általában Fourier-sor, ha az eredeti függvényt egy valós eredménye reprezentálja fizikai dimenzió, mindig konvergálnak. Ennek a folyamatnak a konvergenciájának kérdése bizonyos függvényosztályok esetében új szakaszok megjelenéséhez vezetett a matematikában, például az általánosított függvények elmélete. Olyan nevekkel hozták kapcsolatba, mint L. Schwartz, J. Mikusinsky és J. Temple. Ezen elmélet keretein belül egy világos és pontos elméleti háttér olyan kifejezések alatt, mint a Dirac-delta-függvény (egyetlen terület egy régióját írja le, amely egy pont végtelenül kicsiny környékére koncentrálódik) és Heaviside „lépése”. Ennek a munkának köszönhetően a Fourier-sorok alkalmazhatóvá váltak olyan egyenletek és problémák megoldására, amelyekben intuitív fogalmak jelennek meg: ponttöltés, ponttömeg, mágneses dipólusok, valamint a nyaláb koncentrált terhelése.
A Fourier-sorok, az interferencia elveinek megfelelően, az összetett formák egyszerűbb formákra való bontásával kezdődnek. Például a hőáram változását azzal magyarázzák, hogy egy hőszigetelő anyagból különböző akadályokon halad át. szabálytalan alakú vagy a föld felszínének változása - földrengés, égitest pályájának változása - a bolygók hatása. Az egyszerű klasszikus rendszereket leíró hasonló egyenleteket általában minden egyes hullámra elemileg megoldják. Fourier megmutatta egyszerű megoldásokössze is foglalható, hogy megoldást kapjunk összetettebb problémákra. A matematika nyelvén kifejezve a Fourier-sor egy olyan technika, amely egy kifejezést harmonikusok - koszinusz és szinuszos - összegeként ábrázol. Ezért ezt az elemzést más néven "harmonikus elemzés".
A számítástechnika megalkotása előtt a Fourier-technika volt legjobb fegyver a tudósok arzenáljában, amikor világunk hullámtermészetével dolgozunk. Fourier sorozat be összetett forma lehetővé teszi, hogy nem csak egyszerű feladatokat, amelyek alkalmasak a newtoni mechanika törvényeinek közvetlen alkalmazására, hanem alapegyenletek. A 19. századi newtoni tudomány legtöbb felfedezését csak Fourier technikája tette lehetővé.
A számítógépek fejlődésével a Fourier-transzformációk minőségileg új szintre emelkedtek. Ez a technika a tudomány és a technológia szinte minden területén szilárdan beépült. Ilyen például a digitális audio- és videojel. Megvalósítása csak egy francia matematikus által a 19. század elején kidolgozott elméletnek köszönhetően vált lehetségessé. Így a Fourier-sor összetett formában lehetővé tette az áttörést a vizsgálatban világűr. Ezenkívül ez befolyásolta a félvezető anyagok és a plazma fizikájának, a mikrohullámú akusztikának, az oceanográfiának, a radarnak és a szeizmológiának a tanulmányozását.
A matematikában a Fourier-sor az önkényes ábrázolás módja összetett funkciók az egyszerűbbek összege. NÁL NÉL gyakori esetek az ilyen kifejezések száma végtelen lehet. Sőt, minél jobban figyelembe veszik számukat a számítás során, annál pontosabb a végeredmény. Leggyakrabban a legegyszerűbbként használják trigonometrikus függvények koszinusz vagy szinusz. Ebben az esetben a Fourier-sorokat trigonometrikusnak, az ilyen kifejezések megoldását pedig a harmonikus kiterjesztésének nevezzük. Ez a módszer fontos szerepet játszik a matematikában. A trigonometrikus sorozat mindenekelőtt eszközt ad a képalkotáshoz, valamint a függvények tanulmányozásához, ez az elmélet fő apparátusa. Ezenkívül lehetővé teszi számos matematikai fizika probléma megoldását. Végül ez az elmélet hozzájárult a fejlődéshez, és számos nagyon fontos szakaszt életre hívott matematikai tudomány(az integrálok elmélete, a periodikus függvények elmélete). Emellett kiindulópontul szolgált egy valós változó alábbi függvényeinek kidolgozásához, és egyben a harmonikus elemzés kezdetét is jelentette.
