

Este artigo: “Segundo limite maravilhoso» dedica-se à divulgação dentro dos limites das incertezas da forma:
$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ e $ ^\infty $.
Além disso, tais incertezas podem ser reveladas usando o logaritmo da função exponencial, mas este é outro método de solução, que será abordado em outro artigo.
Fórmula o segundo limite notável é escrito da seguinte forma: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( where ) e \approx 2.718 $$
Segue da fórmula consequências, que são muito convenientes de usar para resolver exemplos com limites: $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( onde ) k \in \mathbb(R) $$ $$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e $ $ $$ \lim_(x \to 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$
Vale ressaltar que o segundo limite notável nem sempre pode ser aplicado a uma função exponencial, mas apenas nos casos em que a base tende à unidade. Para fazer isso, primeiro calcule mentalmente o limite da base e depois tire conclusões. Tudo isso será discutido em soluções de exemplo.
Vejamos exemplos de soluções usando a fórmula direta e suas consequências. Analisaremos também os casos em que a fórmula não é necessária. Basta anotar apenas uma resposta pronta.
| Exemplo 1 |
| Encontre o limite $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ |
| Solução |
|
Vamos substituir o infinito no limite e olhar para a incerteza: $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\frac (\infty)(\infty)\bigg)^\infty $$ Vamos encontrar o limite da base: $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac (4)() x)))(x(1+\frac(3)(x))) = 1 $$ Obtivemos uma base igual a um, o que significa que já podemos aplicar o segundo limite notável. Para fazer isso, vamos ajustar a base da função à fórmula subtraindo e adicionando um: $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ Observamos o segundo corolário e anotamos a resposta: $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ Se você não conseguir resolver seu problema, envie-nos. Forneceremos uma solução detalhada. Você poderá visualizar o andamento do cálculo e obter informações. Isso o ajudará a obter a nota do seu professor em tempo hábil! |
| Responder |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ |
| Exemplo 4 |
| Resolva o limite $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $ |
| Solução |
|
Encontramos o limite da base e vemos que $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1 $, o que significa que podemos aplicar o segundo limite notável. De acordo com o plano padrão, adicionamos e subtraímos um da base do grau: $$ \lim_(x\to \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ Ajustamos a fração à fórmula da 2ª nota. limite: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ Agora vamos ajustar o grau. A potência deve conter uma fração igual ao denominador da base $ \frac(3x^2-2)(6) $. Para fazer isso, multiplique e divida o grau por ele e continue resolvendo: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ O limite localizado na potência em $ e $ é igual a: $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0 $. Portanto, continuando a solução temos: |
| Responder |
| $$ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$ |
Vejamos os casos em que o problema é semelhante ao segundo limite notável, mas pode ser resolvido sem ele.
No artigo: “O Segundo Limite Notável: Exemplos de Soluções” foram analisadas a fórmula, suas consequências e apresentados tipos comuns de problemas neste tema.
Existem vários limites notáveis, mas os mais famosos são o primeiro e o segundo limites notáveis. O que é notável sobre esses limites é que eles são amplamente utilizados e com sua ajuda é possível encontrar outros limites encontrados em vários problemas. Isso é o que faremos na parte prática desta lição. Para resolver problemas reduzindo-os ao primeiro ou segundo limite notável, não há necessidade de revelar as incertezas neles contidas, uma vez que os valores desses limites já foram deduzidos há muito tempo por grandes matemáticos.
O primeiro limite notávelé chamado de limite da razão entre o seno de um arco infinitesimal e o mesmo arco, expresso em radianos:
Vamos prosseguir para a resolução de problemas no primeiro limite notável. Nota: se houver uma função trigonométrica sob o sinal limite, isso é quase sinal certo que esta expressão pode ser levada ao seu primeiro limite notável.
Exemplo 1. Encontre o limite.
Solução. Substituição em vez disso x zero leva à incerteza:
![]() .
.
O denominador é seno, portanto, a expressão pode ser levada ao primeiro limite notável. Vamos começar a transformação:
![]() .
.
O denominador é o seno de três X, mas o numerador tem apenas um X, o que significa que você precisa obter três X no numerador. Para que? Para apresentar 3 x = um e obtenha a expressão .
E chegamos a uma variação do primeiro limite notável:
porque não importa qual letra (variável) nesta fórmula representa em vez de X.
Multiplicamos X por três e dividimos imediatamente:
 .
.
De acordo com o primeiro limite notável observado, substituímos a expressão fracionária:
Agora podemos finalmente resolver este limite:
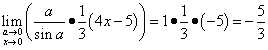 .
.
Exemplo 2. Encontre o limite.
Solução. A substituição direta novamente leva à incerteza “zero dividido por zero”:
![]() .
.
Para obter o primeiro limite notável, é necessário que x sob o sinal de seno no numerador e apenas x no denominador tenham o mesmo coeficiente. Seja este coeficiente igual a 2. Para isso, imagine o coeficiente atual para x conforme abaixo, realizando operações com frações, obtemos:
 .
.
Exemplo 3. Encontre o limite.
Solução. Ao substituir, obtemos novamente a incerteza “zero dividido por zero”:
 .
.
Você provavelmente já entendeu que a partir da expressão original você pode obter o primeiro limite maravilhoso multiplicado pelo primeiro limite maravilhoso. Para fazer isso, decompomos os quadrados de x no numerador e o seno no denominador em fatores idênticos e, para obter os mesmos coeficientes para x e seno, dividimos x no numerador por 3 e multiplicamos imediatamente por 3. Obtemos:
 .
.
Exemplo 4. Encontre o limite.
Solução. Mais uma vez obtemos a incerteza “zero dividido por zero”:
![]() .
.
Podemos obter a razão dos dois primeiros limites notáveis. Dividimos o numerador e o denominador por x. Então, para que os coeficientes de senos e xes coincidam, multiplicamos o x superior por 2 e imediatamente dividimos por 2, e multiplicamos o x inferior por 3 e imediatamente dividimos por 3. Obtemos:

Exemplo 5. Encontre o limite.
Solução. E novamente a incerteza de “zero dividido por zero”:
Lembramos da trigonometria que tangente é a razão entre seno e cosseno, e o cosseno de zero é igual a um. Realizamos as transformações e obtemos:
 .
.
Exemplo 6. Encontre o limite.
Solução. A função trigonométrica sob o sinal de limite sugere novamente o uso do primeiro limite notável. Nós o representamos como a razão entre seno e cosseno.
Esta calculadora matemática online irá ajudá-lo se você precisar calcular o limite de uma função. Programa limites da solução não apenas dá a resposta ao problema, mas também leva solução detalhada com explicações, ou seja exibe o processo de cálculo do limite.
Este programa pode ser útil para estudantes do ensino médio escolas secundárias em preparação para testes e exames, ao testar conhecimentos antes do Exame Estadual Unificado, para os pais controlarem a solução de muitos problemas de matemática e álgebra. Ou talvez seja muito caro contratar um tutor ou comprar novos livros? Ou você apenas quer fazer isso o mais rápido possível? trabalho de casa
em matemática ou álgebra? Neste caso, você também pode utilizar nossos programas com soluções detalhadas.
Desta forma, você pode realizar sua própria formação e/ou formação de seus irmãos ou irmãs mais novos, enquanto aumenta o nível de escolaridade na área de resolução de problemas. Calcular limite
Foi descoberto que alguns scripts necessários para resolver este problema não foram carregados e o programa pode não funcionar.
Você pode ter o AdBlock ativado.
Aqui estão instruções sobre como habilitar o JavaScript em seu navegador.
Porque Tem muita gente disposta a resolver o problema, seu pedido ficou na fila.
Em alguns segundos a solução aparecerá abaixo. Por favor, aguarde
segundo... Se você notei um erro na solução
, então você pode escrever sobre isso no Formulário de Feedback. Não se esqueça indique qual tarefa você decide o que.
entre nos campos
Limite da função em x->x 0
Deixe a função f(x) ser definida em algum conjunto X e deixe o ponto \(x_0 \in X\) ou \(x_0 \notin X\)
Tomemos de X uma sequência de pontos diferente de x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
convergindo para x*. Os valores da função nos pontos desta sequência também formam uma sequência numérica
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
e pode-se levantar a questão da existência do seu limite. Definição
. O número A é chamado de limite da função f(x) no ponto x = x 0 (ou em x -> x 0), se para qualquer sequência (1) de valores do argumento x diferente de x 0 convergindo para x 0, a sequência correspondente (2) da função de valores converge para o número A.
$$ \lim_(x\to x_0)( f(x)) = A $$
A função f(x) pode ter apenas um limite no ponto x 0. Isto decorre do fato de que a sequência
(f(x n)) tem apenas um limite.
e pode-se levantar a questão da existência do seu limite. O número A é chamado de limite da função f(x) no ponto x = x 0 se para qualquer número \(\varepsilon > 0\) existe um número \(\delta > 0\) tal que para todo \ (x \in X, \; x \neq x_0 \), satisfazendo a desigualdade \(|x-x_0| Usando símbolos lógicos, esta definição pode ser escrita na forma
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Observe que as desigualdades \(x \neq x_0 , \; |x-x_0| A primeira definição é baseada no conceito de limite de uma sequência numérica, por isso é frequentemente chamada de definição “na linguagem das sequências”. \(\varepsilon - \delta \)”.
Estas duas definições do limite de uma função são equivalentes e você pode usar qualquer uma delas dependendo de qual for mais conveniente para resolver um problema específico.
Observe que a definição do limite de uma função “na linguagem de sequências” também é chamada de definição do limite de uma função segundo Heine, e a definição do limite de uma função “na linguagem \(\varepsilon - \delta \)” também é chamada de definição do limite de uma função segundo Cauchy.
A seguir, usaremos os conceitos de limites unilaterais de uma função, que são definidos a seguir.
e pode-se levantar a questão da existência do seu limite. O número A é chamado de limite direito (esquerdo) da função f(x) no ponto x 0 se para qualquer sequência (1) convergindo para x 0, cujos elementos x n são maiores (menores que) x 0, a sequência correspondente (2) converge para A.
Simbolicamente está escrito assim:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$
Podemos dar uma definição equivalente de limites unilaterais de uma função “na linguagem \(\varepsilon - \delta \)”:
e pode-se levantar a questão da existência do seu limite. um número A é chamado de limite direito (esquerdo) da função f(x) no ponto x 0 se para qualquer \(\varepsilon > 0\) existe \(\delta > 0\) tal que para todo x satisfatório as desigualdades \(x_0 Entradas simbólicas:
Neste tópico analisaremos as fórmulas que podem ser obtidas usando o segundo limite maravilhoso (localiza-se um tópico dedicado diretamente ao segundo limite maravilhoso). Deixe-me lembrá-lo de duas formulações do segundo limite notável que serão necessárias nesta seção: $\lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e $ e $\lim_(x \to\ 0)\left(1+x\right)^\frac(1)(x)=e$.
Normalmente apresento fórmulas sem comprovação, mas para esta página acho que abrirei uma exceção. A questão é que a prova das consequências do segundo limite notável contém algumas técnicas que são úteis na resolução direta de problemas. Pois bem, de modo geral, é aconselhável saber como se comprova esta ou aquela fórmula. Isso nos permite entender melhor estrutura interna, bem como os limites de aplicabilidade. Mas como as evidências podem não interessar a todos os leitores, irei ocultá-las sob as notas localizadas após cada consequência.
Evidência do corolário nº 1: mostrar\ocultar
Como em $x\to 0$ temos $\ln(1+x)\to 0$, então no limite em consideração há uma incerteza da forma $\frac(0)(0)$. Para revelar essa incerteza, vamos apresentar a expressão $\frac(\ln(1+x))(x)$ na seguinte forma: $\frac(1)(x)\cdot\ln(1+x)$ . Agora vamos fatorar $\frac(1)(x)$ na potência da expressão $(1+x)$ e aplicar o segundo limite notável:
$$ \lim_(x\to\ 0) \frac(\ln(1+x))(x)=\esquerda| \frac(0)(0) \right|= \lim_(x\to\ 0) \left(\frac(1)(x)\cdot\ln(1+x)\right)=\lim_(x\ para\ 0)\ln(1+x)^(\frac(1)(x))=\ln e=1. $$
Mais uma vez temos uma incerteza da forma $\frac(0)(0)$. Contaremos com a fórmula que já provamos. Como $\log_a t=\frac(\ln t)(\ln a)$, então $\log_a (1+x)=\frac(\ln(1+x))(\ln a)$.
$$ \lim_(x\to\ 0) \frac(\log_a (1+x))(x)=\esquerda| \frac(0)(0) \right|=\lim_(x\to\ 0)\frac(\ln(1+x))( x \ln a)=\frac(1)(\ln a)\ lim_(x\to\ 0)\frac(\ln(1+x))( x)=\frac(1)(\ln a)\cdot 1=\frac(1)(\ln a). $$
Evidência do corolário nº 2: mostrar\ocultar
Como em $x\to 0$ temos $e^x-1\to 0$, então no limite em consideração há uma incerteza da forma $\frac(0)(0)$. Para revelar esta incerteza, vamos mudar a variável, denotando $t=e^x-1$. Como $x\para 0$, então $t\para 0$. A seguir, a partir da fórmula $t=e^x-1$ obtemos: $e^x=1+t$, $x=\ln(1+t)$.
$$ \lim_(x\to\ 0) \frac(e^x-1)(x)=\esquerda| \frac(0)(0) \direita|=\esquerda | \begin(alinhado) & t=e^x-1;\; t\to 0.\\ & x=\ln(1+t).\end (aligned) \right|= \lim_(t\to 0)\frac(t)(\ln(1+t))= \lim_(t\to 0)\frac(1)(\frac(\ln(1+t))(t))=\frac(1)(1)=1. $$
Mais uma vez temos uma incerteza da forma $\frac(0)(0)$. Contaremos com a fórmula que já provamos. Como $a^x=e^(x\ln a)$, então:
$$ \lim_(x\to\ 0) \frac(a^(x)-1)(x)=\left| \frac(0)(0) \right|=\lim_(x\to 0)\frac(e^(x\ln a)-1)(x)=\ln a\cdot \lim_(x\to 0 )\frac(e^(x\ln a)-1)(x \ln a)=\ln a \cdot 1=\ln a. $$
Evidência do corolário nº 3: mostrar\ocultar
Mais uma vez estamos lidando com uma incerteza da forma $\frac(0)(0)$. Como $(1+x)^\alpha=e^(\alpha\ln(1+x))$, obtemos:
$$ \lim_(x\to\ 0) \frac((1+x)^\alpha-1)(x)= \left| \frac(0)(0) \right|= \lim_(x\to\ 0)\frac(e^(\alpha\ln(1+x))-1)(x)= \lim_(x\to \ 0)\left(\frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x))\cdot \frac(\alpha\ln(1+x) )(x) \right)=\\ =\alpha\lim_(x\to\ 0) \frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x ))\cdot \lim_(x\to\ 0)\frac(\ln(1+x))(x)=\alpha\cdot 1\cdot 1=\alpha. $$
Exemplo nº 1
Calcule o limite $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)$.
Temos uma incerteza da forma $\frac(0)(0)$. Para revelar essa incerteza, usaremos a fórmula. Para ajustar o nosso limite a esta fórmula, devemos ter em mente que as expressões na potência de $e$ e no denominador devem coincidir. Em outras palavras, não há lugar para o seno no denominador. O denominador deve ser $9x$. Além disso, a solução deste exemplo utilizará o primeiro limite notável.
$$ \lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\left|\frac(0)(0) \right|=\lim_(x\to\ 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(9x)(\sin 5x) \right) =\frac(9)(5)\cdot\lim_(x\ para\ 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(1)(\frac(\sin 5x)(5x)) \right)=\frac(9)( 5)\cdot 1 \cdot 1=\frac(9)(5). $$
Responder: $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\frac(9)(5)$.
Exemplo nº 2
Calcule o limite $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)$.
Temos uma incerteza da forma $\frac(0)(0)$ (deixe-me lembrá-lo que $\ln\cos 0=\ln 1=0$). Para revelar essa incerteza, usaremos a fórmula. Primeiro, vamos levar em conta que $\cos x=1-2\sin^2 \frac(x)(2)$ (veja a impressão sobre funções trigonométricas). Agora $\ln\cos x=\ln\left(1-2\sin^2 \frac(x)(2)\right)$, então no denominador devemos obter a expressão $-2\sin^2 \ frac(x )(2)$ (para ajustar nosso exemplo à fórmula). Na solução posterior, será utilizado o primeiro limite notável.
$$ \lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=\esquerda| \frac(0)(0) \right|=\lim_(x\to\ 0) \frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(x ^2)= \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x)(2))\cdot\frac(-2\sin^2 \frac(x)(2))(x^2) \right)=\\ =-\frac(1)(2) \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x )(2))\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)(2))\right)^2 \right)=-\frac(1)( 2)\cdot 1\cdot 1^2=-\frac(1)(2). $$
Responder: $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=-\frac(1)(2)$.
Agora, com a alma calma, vamos considerar limites maravilhosos.
parece.
Em vez da variável x pode haver várias funções, o principal é que tendem a 0.
É necessário calcular o limite
Como você pode ver, esse limite é muito parecido com o primeiro maravilhoso, mas isso não é inteiramente verdade. Em geral, se você notar um pecado no limite, você deve pensar imediatamente se é possível usar o primeiro limite notável.
De acordo com nossa regra nº 1, substituímos zero em vez de x:
Ficamos com incerteza.
Agora vamos tentar organizar nós mesmos o primeiro limite maravilhoso. Para fazer isso, vamos fazer uma combinação simples:
Então organizamos o numerador e o denominador para destacar 7x. Agora, o familiar limite notável já apareceu. É aconselhável destacá-lo na hora de decidir:
Vamos substituir a solução do primeiro exemplo maravilhoso e obtemos:
Simplificando a fração:
Resposta: 7/3.
Como você pode ver, tudo é muito simples.
Parece , onde e = 2,718281828... é um número irracional.
Várias funções podem estar presentes no lugar da variável x, o principal é que tendem a .
É necessário calcular o limite
Aqui vemos a presença de um grau sob o sinal de um limite, o que significa que é possível utilizar um segundo limite notável.
Como sempre, usaremos a regra nº 1 - substitua x em vez de:
Pode-se ver que em x a base do grau é, e o expoente é 4x >, ou seja, obtemos uma incerteza da forma:
Vamos usar o segundo limite maravilhoso para revelar a nossa incerteza, mas primeiro precisamos organizá-la. Como você pode ver, precisamos conseguir presença no indicador, para o qual elevamos a base à potência de 3x, e ao mesmo tempo à potência de 1/3x, para que a expressão não mude:
Não se esqueça de destacar nosso maravilhoso limite:
Isso é o que eles realmente são limites maravilhosos!
Se você ainda tiver alguma dúvida sobre o primeiro e o segundo limites maravilhosos e fique à vontade para perguntar nos comentários.
Responderemos a todos na medida do possível.
Você também pode trabalhar com um professor neste tópico.
Temos o prazer de oferecer a você os serviços de seleção de um tutor qualificado em sua cidade. Nossos parceiros selecionarão rapidamente um bom professor para você em condições favoráveis.
Não há informações suficientes? - Você pode!
Você pode escrever cálculos matemáticos em blocos de notas. É muito mais agradável escrever individualmente em cadernos com logotipo (http://www.blocnot.ru).