Il numero r è detto rango della matrice A se:
1) la matrice A contiene un minore diverso da zero di ordine r;
2) tutti i minori di ordine (r + 1) e superiori, se esistono, sono uguali a zero.
Altrimenti, il rango di una matrice è l'ordine più alto di un minore diverso da zero.
Designazioni: rangA , r A o r .
Dalla definizione segue che r è un numero intero positivo. Per una matrice nulla, il rango è considerato pari a zero.
Assegnazione del servizio. Il calcolatore online è progettato per trovare rango di matrice. La soluzione viene salvata in formato Word ed Excel. vedi esempio di soluzione.
Istruzione. Selezionare la dimensione della matrice, fare clic su Avanti.
Definizione. Sia data una matrice di rango r. Qualsiasi matrice minore diversa da zero e di ordine r è chiamata base, e le righe e le colonne dei suoi componenti sono chiamate righe e colonne di base.
Secondo questa definizione, la matrice A può avere diverse basi minori.
Rango matrice identità E è uguale a n (numero di righe).
Esempio 1 . Date due matrici, e i loro minori 
, 
. Quale di loro può essere preso come base?
Soluzione. Il minore M 1 =0, quindi non può essere una base per nessuna delle matrici. Minore M 2 =-9≠0 e ha ordine 2, quindi può essere presa come matrice base di A o / e B, purché abbiano rango pari a 2 . Poiché detB=0 (come determinante con due colonne proporzionali), allora rangB=2 e M 2 possono essere presi come base minore della matrice B. Il rango della matrice A è 3, per il fatto che detA=-27≠ 0 e, quindi, l'ordine della base minore di questa matrice deve essere 3, cioè M 2 non è una base per la matrice A . Si noti che la matrice A ha un'unica base minore uguale al determinante della matrice A .
Teorema (sulla base minore).
Qualsiasi riga (colonna) di una matrice è una combinazione lineare delle sue righe (colonne) di base.
Conseguenze del teorema.
Esempio 2 . Trova il rango di una matrice 
.
Soluzione.
Sulla base della definizione del rango di una matrice, cercheremo un minore di ordine massimo diverso da zero. Innanzitutto, trasformiamo la matrice in more in piena vista. Per fare ciò, moltiplica la prima riga della matrice per (-2) e aggiungi alla seconda, quindi moltiplicala per (-1) e aggiungi alla terza.
Per lavorare con il concetto di rango di una matrice, abbiamo bisogno di informazioni dall'argomento "Complementi algebrici e minori. Tipi di minori e complementi algebrici" . Si tratta anzitutto del termine "matrice minore", poiché determineremo il rango di una matrice proprio attraverso le minori.
Rango della matrice indicare l'ordine massimo dei suoi minori, tra i quali ce n'è almeno uno diverso da zero.
Matrici equivalenti sono matrici i cui ranghi sono uguali tra loro.
Spieghiamo più in dettaglio. Supponiamo che tra i minori di secondo ordine ce ne sia almeno uno diverso da zero. E tutti i minori, il cui ordine è superiore a due, sono uguali a zero. Conclusione: il rango della matrice è 2. Oppure, ad esempio, tra i minori del decimo ordine ce n'è almeno uno diverso da zero. E tutti i minori, il cui ordine è superiore a 10, sono uguali a zero. Conclusione: il rango della matrice è 10.
Il rango della matrice $A$ è indicato come segue: $\rang A$ o $r(A)$. Il rango della matrice zero $O$ è posto uguale a zero, $\rang O=0$. Permettetemi di ricordarvi che per formare una matrice minore è necessario barrare righe e colonne, ma è impossibile barrare più righe e colonne di quante ne contenga la matrice stessa. Ad esempio, se la matrice $F$ ha dimensione $5\volte 4$ (cioè contiene 5 righe e 4 colonne), allora l'ordine massimo dei suoi minori è quattro. Non sarà più possibile formare minori di quinto ordine, poiché richiederanno 5 colonne (e noi ne abbiamo solo 4). Ciò significa che il rango della matrice $F$ non può essere maggiore di quattro, cioè $\rang F≤4$.
In una forma più generale, quanto sopra significa che se la matrice contiene $m$ righe e $n$ colonne, allora il suo rango non può superare il più piccolo dei numeri $m$ e $n$, cioè $\rang A≤\min(m,n)$.
In linea di principio, il metodo per trovarlo deriva dalla definizione stessa del rango. Il processo di ricerca del rango di una matrice per definizione può essere rappresentato schematicamente come segue:
Permettetemi di spiegare questo diagramma in modo più dettagliato. Cominciamo a ragionare dall'inizio, ad es. con minori di primo ordine di qualche matrice $A$.
Cosa ci aspetta al termine di questa procedura? È possibile che tra i minori del k-esimo ordine ce ne sia almeno uno diverso da zero, e tutti i minori del (k + 1)esimo ordine saranno uguali a zero. Ciò significa che k è l'ordine massimo di minori tra i quali ce n'è almeno uno diverso da zero, cioè il rango sarà uguale a k. Ci può essere una situazione diversa: tra i minori del k-esimo ordine ce ne sarà almeno uno diverso da zero, e i minori del (k + 1)esimo ordine non possono formarsi. Anche in questo caso il rango della matrice è uguale a k. Insomma, l'ordine dell'ultimo minore diverso da zero composto e sarà uguale al rango della matrice.
Passiamo agli esempi in cui verrà illustrato chiaramente il processo di ricerca del rango di una matrice per definizione. Sottolineo ancora una volta che negli esempi di questo argomento troveremo il rango delle matrici utilizzando solo la definizione del rango. Altri metodi (calcolo del rango di una matrice con il metodo dei minori confinanti, calcolo del rango di una matrice con il metodo delle trasformazioni elementari) sono considerati nei seguenti argomenti.
A proposito, non è affatto necessario avviare la procedura per trovare il grado dai minori dell'ordine più piccolo, come è stato fatto negli esempi n. 1 e n. 2. Puoi rivolgerti subito ai minori di ordine superiore (vedi esempio n. 3).
Esempio 1
Trova il rango di una matrice $A=\left(\begin(array)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(array)\right)$.
Questa matrice ha dimensione $3\volte 5$, cioè contiene tre righe e cinque colonne. Dei numeri 3 e 5, 3 è il minimo, quindi il rango della matrice $A$ è al massimo 3, cioè $\classifica A≤ 3$. E questa disuguaglianza è ovvia, poiché non possiamo più formare minori del quarto ordine: hanno bisogno di 4 righe e ne abbiamo solo 3. Procediamo direttamente al processo di ricerca del rango di una data matrice.
Tra i minori del primo ordine (cioè tra gli elementi della matrice $A$) ce ne sono di diversi da zero. Ad esempio, 5, -3, 2, 7. In generale, non siamo interessati al numero totale di elementi diversi da zero. C'è almeno un elemento diverso da zero e questo è sufficiente. Poiché c'è almeno un diverso da zero tra i minori di primo ordine, concludiamo che $\rang A≥ 1$ e procediamo a controllare i minori di secondo ordine.
Cominciamo ad esplorare i minori di secondo ordine. Ad esempio, all'intersezione delle righe #1, #2 e delle colonne #1, #4 ci sono elementi del seguente minore: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end (array) \destra| $. Per questo determinante, tutti gli elementi della seconda colonna sono uguali a zero, quindi il determinante stesso è uguale a zero, cioè $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=0$ (vedi proprietà #3 nella proprietà dei determinanti). Oppure puoi semplicemente calcolare questo determinante usando la formula n. 1 dalla sezione sul calcolo dei determinanti di secondo e terzo ordine:
$$ \left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=5\cdot 0-0\cdot 7=0. $$
Il primo minore del secondo ordine che abbiamo controllato è risultato essere uguale a zero. Cosa dice? Sulla necessità di verificare ulteriormente i minori di secondo grado. O risultano tutti zero (e quindi il rango sarà uguale a 1), oppure tra loro c'è almeno un minore diverso da zero. Proviamo a fare una scelta migliore scrivendo un minore di secondo ordine i cui elementi si trovano all'intersezione delle righe #1, #2 e delle colonne #1 e #5: $\left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array)\right|$. Troviamo il valore di questo minore del secondo ordine:
$$ \left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|=5\cdot 3-2\cdot 7=1. $$
Questo minore non è uguale a zero. Conclusione: tra i minori di secondo ordine ce n'è almeno uno diverso da zero. Quindi $\rank A≥ 2$. È necessario procedere allo studio dei minori del terz'ordine.
Se per la formazione dei minori del terzo ordine scegliamo la colonna #2 o la colonna #4, allora tali minori saranno uguali a zero (perché conterranno una colonna zero). Resta da controllare solo un minore del terzo ordine, i cui elementi si trovano all'intersezione delle colonne n. 1, n. 3, n. 5 e righe n. 1, n. 2, n. Scriviamo questo minore e troviamo il suo valore:
$$ \left|\begin(array)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(array) \right|=-20-18-14 +16+21+15=0. $$
Quindi, tutti i minori di terzo ordine sono uguali a zero. L'ultimo minore diverso da zero che abbiamo compilato era di secondo ordine. Conclusione: l'ordine massimo dei minori, tra i quali ce n'è almeno uno diverso da zero, è pari a 2. Pertanto, $\rang A=2$.
Risposta: $\grado A=2$.
Esempio #2
Trova il rango di una matrice $A=\left(\begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 & 7 & 8 & -7 \end(array) \right)$.
abbiamo matrice quadrata quarto ordine. Notiamo subito che il rango di questa matrice non supera 4, cioè $\classifica A≤ 4$. Iniziamo a trovare il rango di una matrice.
Tra i minori del primo ordine (cioè tra gli elementi della matrice $A$) ce n'è almeno uno diverso da zero, quindi $\rang A≥ 1$. Si passa alla verifica dei minori di secondo ordine. Ad esempio, all'intersezione delle righe n. 2, n. 3 e delle colonne n. 1 e n. 2, otteniamo il seguente minore del secondo ordine: $\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|$. Calcoliamolo:
$$ \sinistra| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|=0-10=-10. $$
Tra le minori di secondo ordine ce n'è almeno una che non è uguale a zero, quindi $\rang A≥ 2$.
Passiamo ai minori di terz'ordine. Troviamo, ad esempio, un minore i cui elementi si trovano all'intersezione delle righe n. 1, n. 3, n. 4 e colonne n. 1, n. 2, n. 4:
$$ \sinistra | \begin(array) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(array) \right|=105-105=0. $$
Poiché questo minore di terzo ordine è risultato uguale a zero, è necessario indagare su un altro minore di terzo ordine. O saranno tutti uguali a zero (quindi il rango sarà uguale a 2), oppure tra loro ce ne sarà almeno uno diverso da zero (allora inizieremo a studiare i minori del quarto ordine). Considera un minore di terzo ordine i cui elementi si trovano all'intersezione delle righe n. 2, n. 3, n. 4 e colonne n. 2, n. 3, n. 4:
$$ \sinistra| \begin(array) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(array) \right|=-28. $$
C'è almeno un minore diverso da zero tra i minori di terzo ordine, quindi $\rang A≥ 3$. Passiamo alla verifica dei minori di quarto ordine.
Qualsiasi minore del quarto ordine si trova all'intersezione di quattro righe e quattro colonne della matrice $A$. In altre parole, il minore di quarto ordine è il determinante della matrice $A$, poiché questa matrice contiene solo 4 righe e 4 colonne. Il determinante di questa matrice è stato calcolato nell'esempio n. 2 dell'argomento "Riduzione dell'ordine del determinante. Decomposizione del determinante in una riga (colonna)" , quindi prendiamo solo il risultato finale:
$$ \sinistra| \begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (array)\destra|=86. $$
Quindi, il minore di quarto ordine non è uguale a zero. Non possiamo più formare minori di quinto ordine. Conclusione: il più alto ordine di minori, tra cui ce n'è almeno uno diverso da zero, è 4. Risultato: $\rang A=4$.
Risposta: $\grado A=4$.
Esempio #3
Trova il rango di una matrice $A=\left(\begin(array) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end(array)\destra)$.
Nota subito che questa matrice contiene 3 righe e 4 colonne, quindi $\rang A≤ 3$. Negli esempi precedenti, abbiamo avviato il processo di ricerca del rango considerando i minori del più piccolo (primo) ordine. Qui proveremo a controllare immediatamente i minori dell'ordine più alto possibile. Per la matrice $A$, questi sono minori di terzo ordine. Considera un minore di terzo ordine i cui elementi si trovano all'intersezione delle righe n. 1, n. 2, n. 3 e colonne n. 2, n. 3, n. 4:
$$ \sinistra| \begin(array) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(array) \right|=-8-60-20=-88. $$
Quindi, l'ordine più alto dei minori, tra i quali ce n'è almeno uno diverso da zero, è 3. Pertanto, il rango della matrice è 3, ovvero $\classifica A=3$.
Risposta: $\grado A=3$.
In generale, trovare il rango di una matrice per definizione è un problema caso generale il compito è abbastanza noioso. Ad esempio, una matrice $5\volte 4$ relativamente piccola ha 60 minori di secondo ordine. E anche se 59 di loro sono uguali a zero, il 60 ° minore potrebbe risultare diverso da zero. Quindi devi esplorare i minori di terzo ordine, di cui questa matrice ha 40 pezzi. Solitamente si cerca di utilizzare metodi meno macchinosi, come il metodo della confinatura dei minori o il metodo delle trasformazioni equivalenti.
Sia data una matrice:
.
Selezionare in questa matrice 
linee arbitrarie e 
colonne arbitrarie 
. Poi il determinante 
esimo ordine, composto da elementi di matrice 
situato all'intersezione di righe e colonne selezionate è chiamato minore 
-esima matrice di ordine 
.
Definizione 1.13. Rango della matrice 
è l'ordine più grande del minore diverso da zero di questa matrice.
Per calcolare il rango di una matrice occorre considerare tutti i suoi minori di ordine minimo e, se almeno uno di essi è diverso da zero, procedere alla considerazione dei minori di ordine superiore. Questo approccio per determinare il rango di una matrice è chiamato metodo di confine (o metodo dei minori di confine).
Compito 1.4. Con il metodo dei minori confinanti, determinare il rango di una matrice 
.
.
Considera il confine di primo ordine, ad esempio, 
. Poi passiamo alla considerazione di alcuni confini del secondo ordine.
Per esempio, 
.
Infine, analizziamo la bordatura del terzo ordine.
.
Quindi l'ordine più alto di un minore diverso da zero è 2, quindi 
.
Risolvendo il Problema 1.4, si può notare che le serie dei minori confinanti del secondo ordine sono diverse da zero. A questo proposito, ha luogo la seguente nozione.
Definizione 1.14. La base minore di una matrice è qualsiasi minore diverso da zero il cui ordine è uguale al rango della matrice.
Teorema 1.2.(Teorema minore di base). Le righe di base (colonne di base) sono linearmente indipendenti.
Si noti che le righe (colonne) di una matrice sono linearmente dipendenti se e solo se almeno una di esse può essere rappresentata come combinazione lineare delle altre.
Teorema 1.3. Il numero di righe della matrice linearmente indipendenti è uguale al numero di colonne della matrice linearmente indipendenti ed è uguale al rango della matrice.
Teorema 1.4.(Condizione necessaria e sufficiente perché il determinante sia uguale a zero). Per il determinante 
-esimo ordine 
è uguale a zero, è necessario e sufficiente che le sue righe (colonne) siano linearmente dipendenti.
Calcolare il rango di una matrice in base alla sua definizione è troppo macchinoso. Ciò diventa particolarmente importante per le matrici di ordine elevato. A tal proposito, in pratica, il rango di una matrice viene calcolato in base all'applicazione dei Teoremi 10.2 - 10.4, nonché all'utilizzo dei concetti di equivalenza matriciale e trasformazioni elementari.
Definizione 1.15. Due matrici 
e 
sono detti equivalenti se i loro ranghi sono uguali, cioè 
.
Se matrici 
e 
sono equivalenti, quindi nota 
.
Teorema 1.5. Il rango di una matrice non cambia dalle trasformazioni elementari.
Chiameremo trasformazioni elementari della matrice 
una qualsiasi delle seguenti azioni sulla matrice:
Sostituzione di righe con colonne e colonne con righe corrispondenti;
Permutazione di righe di matrici;
Attraversando una linea, i cui elementi sono tutti uguali a zero;
Moltiplicando qualsiasi stringa per un numero diverso da zero;
Sommando agli elementi di una riga gli elementi corrispondenti di un'altra riga moltiplicati per lo stesso numero 
.
Corollario del Teorema 1.5. Se la matrice 
ottenuto dalla matrice 
utilizzando un numero finito di trasformazioni elementari, quindi le matrici 
e 
sono equivalenti.
Quando si calcola il rango di una matrice, dovrebbe essere ridotto a una forma trapezoidale utilizzando un numero finito di trasformazioni elementari.
Definizione 1.16. Chiameremo trapezio una tale forma di rappresentazione della matrice, quando nel minore confinante ordine superiore diverso da zero, tutti gli elementi sotto la diagonale svaniscono. Per esempio:
.
Qui 
, elementi di matrice 
girare a zero. Quindi la forma di rappresentazione di tale matrice sarà trapezoidale.
Di norma, le matrici vengono ridotte a una forma trapezoidale utilizzando l'algoritmo gaussiano. L'idea dell'algoritmo gaussiano è che, moltiplicando gli elementi della prima riga della matrice per i fattori corrispondenti, si ottiene che tutti gli elementi della prima colonna situati sotto l'elemento 
, diventerebbe zero. Quindi, moltiplicando gli elementi della seconda colonna per i moltiplicatori corrispondenti, otteniamo che tutti gli elementi della seconda colonna situati sotto l'elemento 
, diventerebbe zero. Procedi ulteriormente allo stesso modo.
Compito 1.5. Determina il rango di una matrice riducendola a una forma trapezoidale.
.
Per comodità di applicazione dell'algoritmo gaussiano, puoi scambiare la prima e la terza riga.
.
Ovviamente qui 
. Tuttavia, per portare il risultato a una forma più elegante, si possono continuare ulteriori trasformazioni sulle colonne.
.
Definizione. Rango della matriceè il numero massimo di righe linearmente indipendenti considerate come vettori.
Teorema 1 sul rango di una matrice. Rango della matriceè l'ordine massimo di un minore diverso da zero di una matrice.
Abbiamo già discusso il concetto di minore nella lezione sulle determinanti, e ora lo generalizzeremo. Prendiamo alcune righe e alcune colonne nella matrice, e questo "qualcosa" dovrebbe essere inferiore al numero di righe e colonne della matrice, e per righe e colonne questo "qualcosa" dovrebbe essere lo stesso numero. Quindi all'intersezione di quante righe e quante colonne ci sarà una matrice di ordine inferiore rispetto alla nostra matrice originale. Il determinante di questa matrice sarà un k-esimo ordine minore se il citato "qualcosa" (il numero di righe e colonne) è indicato con k.
Definizione. Minore ( r+1)-esimo ordine, all'interno del quale si trova il minore prescelto r-esimo ordine, è chiamato confinante per il dato minore.
I due metodi più comunemente usati trovare il rango di una matrice. esso modo di fringing minori e metodo delle trasformazioni elementari(secondo il metodo di Gauss).
Il metodo dei minori confinanti utilizza il seguente teorema.
Teorema 2 sul rango di una matrice. Se è possibile comporre un minore dagli elementi della matrice r esimo ordine, che non è uguale a zero, allora il rango della matrice è uguale a r.
Con il metodo delle trasformazioni elementari si utilizza la seguente proprietà:
Se per trasformazioni elementari si ottiene una matrice trapezoidale equivalente a quella originaria, allora il rango di questa matriceè il numero di righe in esso ad eccezione delle righe costituite interamente da zeri.
Un minore confinante è un minore di ordine superiore rispetto a quello dato, se questo minore di ordine superiore contiene il minore dato.
Ad esempio, data la matrice
Prendiamo un minore
il bordo sarà tale minori:
Algoritmo per trovare il rango di una matrice prossimo.
1. Troviamo minori di secondo ordine diversi da zero. Se tutti i minori di secondo ordine sono uguali a zero, allora il rango della matrice sarà uguale a uno ( r =1 ).
2. Se esiste almeno un minore di secondo ordine diverso da zero, allora componiamo minori di terzo ordine confinanti. Se tutti i minori confinanti di terzo ordine sono zero, allora il rango della matrice è due ( r =2 ).
3. Se almeno uno dei minori confinanti del terzo ordine non è uguale a zero, allora componiamo i minori confinanti con esso. Se tutti i minori di quarto ordine confinanti sono zero, allora il rango della matrice è tre ( r =2 ).
4. Continua finché la dimensione della matrice lo consente.
Esempio 1 Trova il rango di una matrice
.
Soluzione. Minori di secondo ordine 
.
Lo incorniciamo. I minori confinanti saranno quattro:
,
,
Pertanto, tutti i minori di terzo ordine confinanti sono uguali a zero, quindi il rango di questa matrice è due ( r =2 ).
Esempio 2 Trova il rango di una matrice
Soluzione. Il rango di questa matrice è 1, poiché tutti i minori di secondo ordine di questa matrice sono uguali a zero (in questo, come nei casi di minori confinanti nei prossimi due esempi, i cari studenti sono invitati a verificare di persona, magari utilizzando le regole per il calcolo dei determinanti), e tra i minori di primo ordine, cioè tra gli elementi della matrice, non ci sono uguali a zero.
Esempio 3 Trova il rango di una matrice
Soluzione. Il minore di secondo ordine di questa matrice è e tutti i minori di terzo ordine di questa matrice sono zero. Pertanto, il rango di questa matrice è due.
Esempio 4 Trova il rango di una matrice
Soluzione. Il rango di questa matrice è 3 perché l'unico minore di terzo ordine di questa matrice è 3.
Già nell'Esempio 1 si può vedere che il problema di determinare il rango di una matrice con il metodo dei minori confinanti richiede il calcolo di un gran numero di determinanti. Esiste, tuttavia, un modo per ridurre al minimo la quantità di calcolo. Questo metodo si basa sull'uso di trasformazioni matriciali elementari ed è anche chiamato metodo di Gauss.
Le trasformazioni elementari di una matrice significano le seguenti operazioni:
1) moltiplicazione di qualsiasi riga o colonna della matrice per un numero diverso da zero;
2) sommare agli elementi di una qualsiasi riga o colonna della matrice i corrispondenti elementi di un'altra riga o colonna, moltiplicati per lo stesso numero;
3) scambiare due righe o colonne di una matrice;
4) rimozione delle righe "nulle", ovvero quelle i cui elementi sono tutti uguali a zero;
5) soppressione di tutte le righe proporzionali, tranne una.
Teorema. La trasformazione elementare non cambia il rango della matrice. In altre parole, se usiamo trasformazioni elementari dalla matrice UN vai a matrice B, poi .
E considera anche un'importante applicazione pratica dell'argomento: ricerca di sistema equazioni lineari per compatibilità.
L'epigrafe umoristica dell'articolo contiene una grande quantità di verità. La stessa parola "grado" è solitamente associata a una sorta di gerarchia, molto spesso con la scala della carriera. Maggiore è la conoscenza, l'esperienza, le capacità, le connessioni, ecc. Una persona ha. - maggiore è la sua posizione e la gamma di opportunità. In termini giovanili, il rango si riferisce al grado complessivo di "durezza".
E i nostri fratelli matematici vivono secondo gli stessi principi. Facciamo una passeggiata qualche arbitrario matrici nulle:
Pensiamo se nella matrice solo zeri, allora di quale grado possiamo parlare? Tutti conoscono l'espressione informale "totale zero". Nella società della matrice, tutto è esattamente uguale:
Rango di matrice zeroqualsiasi dimensione è zero.
Nota : la matrice zero è indicata dalla lettera greca "theta"
Per comprendere meglio il rango della matrice, di seguito attingerò ai materiali geometria analitica. Considera zero vettore i nostri spazio tridimensionale, che non stabilisce una direzione specifica ed è inutile per la costruzione base affine. Da un punto di vista algebrico, vengono scritte le coordinate di un dato vettore matrice"uno per tre" e logico (nel senso geometrico specificato) supponiamo che il rango di questa matrice sia zero.
Ora diamo un'occhiata ad alcuni diverso da zero vettori colonna e vettori riga:
Ogni istanza ha almeno un elemento non nullo, e questo è qualcosa!
Il rango di qualsiasi vettore riga diverso da zero (vettore colonna) è uguale a uno
E in generale - se in matrice dimensioni arbitrarie ha almeno un elemento diverso da zero, quindi il suo rango non meno unità.
I vettori riga e colonna algebrici sono in una certa misura astratti, quindi torniamo all'associazione geometrica. diverso da zero vettore stabilisce una direzione ben definita nello spazio ed è adatto alla costruzione base, quindi si assumerà che il rango della matrice sia uguale a uno.
Background teorico : in algebra lineare, un vettore è un elemento di uno spazio vettoriale (definito attraverso 8 assiomi), che, in particolare, può essere una riga (o colonna) ordinata di numeri reali con le operazioni di addizione e moltiplicazione definite per essi da numero reale. Con più informazioni dettagliate sui vettori possono essere trovati nell'articolo Trasformazioni lineari.
linearmente dipendente(espressi l'uno attraverso l'altro). Da un punto di vista geometrico, la seconda riga contiene le coordinate del vettore collineare 
, che non ha portato avanti la questione nella costruzione base tridimensionale, essendo ridondante in questo senso. Pertanto, anche il rango di questa matrice è uguale a uno.
Riscriviamo le coordinate dei vettori in colonne ( trasporre la matrice):
Cosa è cambiato in termini di rango? Niente. Le colonne sono proporzionali, il che significa che il rango è uguale a uno. A proposito, nota che anche tutte e tre le linee sono proporzionali. Possono essere identificati con le coordinate tre vettori collineari del piano, di cui solo uno utile per costruire una base "piatta". E questo è in pieno accordo con il nostro senso geometrico del rango.
Dall'esempio precedente segue un'affermazione importante:
Il rango di una matrice per righe è uguale al rango di una matrice per colonne. Ne ho già parlato un po 'nella lezione sull'efficacia metodi per il calcolo del determinante.
Nota : la dipendenza lineare delle righe porta alla dipendenza lineare delle colonne (e viceversa). Ma per risparmiare tempo, e per abitudine, parlerò quasi sempre della dipendenza lineare delle stringhe.
Continuiamo ad addestrare il nostro amato animale domestico. Aggiungi le coordinate di un altro vettore collineare alla matrice nella terza riga 
:
Ci ha aiutato a costruire una base tridimensionale? Ovviamente no. Tutti e tre i vettori camminano avanti e indietro lungo lo stesso percorso e il rango della matrice è uno. Puoi prendere tutti i vettori collineari che vuoi, diciamo 100, inserire le loro coordinate in una matrice 100 per 3 e il rango di un tale grattacielo rimarrà comunque uno.
Facciamo conoscenza con la matrice le cui righe linearmente indipendente. Una coppia di vettori non allineati è adatta per costruire una base tridimensionale. Il rango di questa matrice è due.
Qual è il rango della matrice? Le linee non sembrano proporzionali...quindi, in teoria, tre. Tuttavia, anche il rango di questa matrice è uguale a due. Ho aggiunto le prime due righe e ho annotato il risultato in fondo, ad es. espresso linearmente terza riga attraverso le prime due. Geometricamente, le righe della matrice corrispondono alle coordinate di tre vettori complanari, e tra questa tripla c'è una coppia di compagni non collineari.
Come potete vedere dipendenza lineare nella matrice considerata non è ovvio, e oggi impareremo solo come portarlo "all'acqua pulita".
Penso che molte persone indovinino qual è il rango di una matrice!
Considera una matrice le cui righe linearmente indipendente. Forma dei vettori base affine, e il rango di questa matrice è tre.
Come sai, qualsiasi quarto, quinto, decimo vettore dello spazio tridimensionale sarà espresso linearmente in termini di vettori di base. Pertanto, se alla matrice viene aggiunto un numero qualsiasi di righe, allora il suo rango saranno ancora tre.
Analogo ragionamento può essere svolto per le matrici dimensioni maggiori(ovviamente, già senza senso geometrico).
Definizione : il rango della matrice è il numero massimo di righe linearmente indipendenti. O: il rango di una matrice è il numero massimo di colonne linearmente indipendenti. Sì, coincidono sempre.
Da quanto sopra segue un'importante linea guida pratica: il rango di una matrice non supera la sua dimensione minima. Ad esempio, nella matrice 
quattro righe e cinque colonne. La dimensione minima è quattro, quindi il rango di questa matrice non supererà sicuramente 4.
Notazione: nella teoria e nella pratica mondiale non esiste uno standard generalmente accettato per designare il rango della matrice, si trova quello più comune: - come si suol dire, un inglese scrive una cosa, un tedesco un'altra. Pertanto, sulla base del noto aneddoto sull'inferno americano e russo, indichiamo il grado della matrice con una parola nativa. Per esempio: . E se la matrice è "senza nome", di cui ce ne sono molte, allora puoi semplicemente scrivere .
Se nostra nonna avesse una quinta colonna nella matrice, allora avrebbe dovuto essere calcolato un altro minore di 4° ordine ("blu", "lampone" + 5a colonna).
Conclusione: l'ordine massimo di un minore diverso da zero è tre, quindi .
Forse non tutti hanno compreso appieno questa frase: il minore di 4° ordine è uguale a zero, ma tra i minori di 3° ordine ce n'era uno diverso da zero - quindi ordine massimo diverso da zero minore e uguale a tre.
La domanda sorge spontanea, perché non calcolare immediatamente il determinante? Ebbene, in primo luogo, nella maggior parte delle attività la matrice non è quadrata e, in secondo luogo, anche se ottieni un valore diverso da zero, l'attività verrà rifiutata con un'alta probabilità, poiché di solito implica un "dal basso verso l'alto" standard soluzione. E nell'esempio considerato, il determinante zero del 4 ° ordine ci consente persino di affermare che il rango della matrice è solo inferiore a quattro.
Devo ammettere che mi sono inventato io stesso il problema analizzato per spiegare meglio il metodo di confinamento dei minori. Nella pratica reale, tutto è più semplice:
Esempio 2
Trova il rango di una matrice con il metodo dei minori marginali 
Soluzione e risposta alla fine della lezione.
Quando l'algoritmo funziona più velocemente? Torniamo alla stessa matrice quattro per quattro 
. Ovviamente la soluzione sarà la più breve nel caso di "buono" minori d'angolo: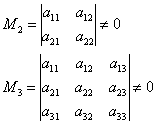
E, se, allora, altrimenti -.
Il pensiero non è affatto ipotetico: ci sono molti esempi in cui il tutto è limitato solo ai minori angolari.
Tuttavia, in alcuni casi, un altro metodo è più efficace e preferibile:
Questa sezione è destinata ai lettori che hanno già familiarità con Metodo di Gauss e piano piano ci hanno messo le mani sopra.
Dal punto di vista tecnico il metodo non è nuovo:
1) utilizzando trasformazioni elementari, portiamo la matrice in una forma a gradino;
2) il rango della matrice è uguale al numero di righe.
È abbastanza chiaro che l'utilizzo del metodo di Gauss non modifica il rango della matrice, e l'essenza qui è estremamente semplice: secondo l'algoritmo, nel corso delle trasformazioni elementari, vengono identificate e rimosse tutte le linee proporzionali (linearmente dipendenti) non necessarie, a seguito delle quali rimane un "residuo secco" - il numero massimo di rette linearmente indipendenti.
Trasformiamo la vecchia matrice familiare con le coordinate di tre vettori collineari: 
(1) La prima riga è stata aggiunta alla seconda riga, moltiplicata per -2. La prima riga è stata aggiunta alla terza riga.
(2) Le linee zero vengono rimosse.
Quindi è rimasta una riga, quindi . Inutile dire che questo è molto più veloce che calcolare nove zero minori del 2° ordine e solo allora trarre una conclusione.
Te lo ricordo di per sé matrice algebrica nulla può essere modificato e le trasformazioni vengono eseguite solo allo scopo di scoprire il rango! A proposito, soffermiamoci di nuovo sulla domanda, perché no? Matrice Sorgente 
trasporta informazioni fondamentalmente diverse dalle informazioni di matrice e riga. In qualche modelli matematici(senza esagerare) la differenza in un numero può essere una questione di vita o di morte. ... Ho ricordato gli insegnanti di matematica della scuola primaria e secondaria, che tagliavano spietatamente il voto di 1-2 punti per la minima imprecisione o deviazione dall'algoritmo. Ed è stato terribilmente deludente quando, invece dei "cinque" apparentemente garantiti, si è rivelato "buono" o anche peggio. La comprensione è arrivata molto più tardi: in quale altro modo affidare a una persona satelliti, testate nucleari e centrali elettriche? Ma non preoccuparti, non lavoro in queste zone =)
Passiamo a compiti più significativi, dove, tra le altre cose, faremo conoscenza con importanti tecniche computazionali Metodo di Gauss:
Esempio 3
Trova il rango di una matrice usando le trasformazioni elementari 
Soluzione: data una matrice quattro per cinque, il che significa che il suo rango non è certamente superiore a 4.
Nella prima colonna non c'è 1 o -1, quindi sono necessari passaggi aggiuntivi per ottenere almeno un'unità. Durante l'intera esistenza del sito, mi è stata ripetutamente posta la domanda: "È possibile riorganizzare le colonne durante le trasformazioni elementari?". Qui - riorganizzato la prima o la seconda colonna, e va tutto bene! Nella maggior parte delle attività dove Metodo di Gauss, le colonne possono davvero essere riorganizzate. MA NON FARLO. E il punto non è nemmeno una possibile confusione con le variabili, il punto è che nel classico corso di studi matematica superiore questa azione tradizionalmente non è considerata, quindi un tale inchino sarà guardato MOLTO storto (o addirittura costretto a rifare tutto).
Il secondo punto riguarda i numeri. Nel corso della decisione, è utile essere guidati dalla seguente regola empirica: le trasformazioni elementari dovrebbero, se possibile, ridurre i numeri della matrice. In effetti, è molto più facile lavorare con uno-due-tre che, ad esempio, con 23, 45 e 97. E la prima azione mira non solo a ottenere un'unità nella prima colonna, ma anche a eliminare i numeri 7 e 11.
Prima la soluzione completa, poi i commenti: 
(1) La prima riga è stata aggiunta alla seconda riga, moltiplicata per -2. La prima riga è stata aggiunta alla terza riga, moltiplicata per -3. E all'heap: la 1a riga, moltiplicata per -1, è stata aggiunta alla 4a riga.
(2) Le ultime tre righe sono proporzionali. Eliminate la 3a e 4a riga, la seconda riga è stata spostata al primo posto.
(3) La prima riga è stata aggiunta alla seconda riga, moltiplicata per -3.
La matrice ridotta a una forma a gradini ha due righe.
Risposta:
Ora tocca a te torturare la matrice quattro per quattro:
Esempio 4
Trova il rango di una matrice usando il metodo gaussiano 
Te lo ricordo Metodo di Gauss non implica una rigidità inequivocabile e molto probabilmente la tua soluzione sarà diversa dalla mia soluzione. Un breve esempio del compito alla fine della lezione.
In pratica, spesso non viene detto affatto quale metodo dovrebbe essere utilizzato per trovare il rango. In una situazione del genere, si dovrebbe analizzare la condizione: per alcune matrici è più razionale eseguire la soluzione attraverso minori, mentre per altre è molto più vantaggioso applicare trasformazioni elementari:
Esempio 5
Trova il rango di una matrice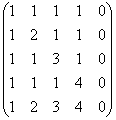 
Soluzione: il primo modo in qualche modo scompare immediatamente =)
Un po 'più in alto, ho consigliato di non toccare le colonne della matrice, ma quando c'è una colonna zero, o colonne proporzionali / corrispondenti, vale comunque la pena amputare: 
(1) La quinta colonna è zero, la togliamo dalla matrice. Pertanto, il rango della matrice è al massimo quattro. La prima riga viene moltiplicata per -1. Questa è un'altra caratteristica distintiva del metodo gaussiano, che rende la seguente azione una piacevole passeggiata:
(2) A tutte le righe, a partire dalla seconda, è stata aggiunta la prima riga.
(3) La prima riga è stata moltiplicata per -1, la terza riga è stata divisa per 2, la quarta riga è stata divisa per 3. La seconda riga moltiplicata per -1 è stata aggiunta alla quinta riga.
(4) La terza riga è stata aggiunta alla quinta riga, moltiplicata per -2.
(5) Le ultime due righe sono proporzionali, cancelliamo la quinta.
Il risultato sono 4 righe.
Risposta:
Edificio standard di cinque piani per l'autoesplorazione:
Esempio 6
Trova il rango di una matrice
Soluzione breve e risposta alla fine della lezione.
Va notato che la frase "matrix rank" non è così comune nella pratica e nella maggior parte dei problemi puoi farne a meno. Ma c'è un compito in cui il concetto in esame è il principale. attore, e alla fine dell'articolo vedremo questa applicazione pratica:
Spesso, oltre a risolvere sistemi di equazioni lineari secondo la condizione, è prima necessario esaminarne la compatibilità, cioè provare che esiste una soluzione. Un ruolo chiave in questa verifica è svolto da Teorema di Kronecker-Capelli, che formulerò nella forma richiesta:
Se rango matrici di sistema uguale al rango sistema a matrice aumentata, allora il sistema è consistente, e se il numero dato coincide con il numero di incognite, allora la soluzione è unica.
Pertanto, per studiare il sistema per la compatibilità, è necessario verificare l'uguaglianza 
, dove - matrice di sistema(ricorda la terminologia della lezione Metodo di Gauss), un - sistema a matrice aumentata(es. matrice con coefficienti alle variabili + colonna di termini liberi).
