Egy r számot az A mátrix rangjának nevezünk, ha:
1) az A mátrixban van egy r rendű, nullától eltérő moll;
2) minden (r+1) és magasabb rendű minor, ha létezik, egyenlő nullával.
Ellenkező esetben a mátrix rangja a nullától eltérő legmagasabb kisebb rendű.
Megnevezések: rangA, r A vagy r.
A definícióból az következik, hogy r pozitív egész szám. Nulla mátrix esetén a rangot nullának tekintjük.
A szolgáltatás célja. Az online számológépet úgy tervezték, hogy megtalálja mátrix rang. Ebben az esetben a megoldás Word és Excel formátumban kerül mentésre. lásd példa megoldás.
Utasítás. Válassza ki a mátrix dimenzióját, majd kattintson a Tovább gombra.
Meghatározás . Legyen adott egy r rangú mátrix. A mátrix nullától eltérő, r sorrendű kisebb részét alapnak, az összetevőinek sorait és oszlopait pedig alapsoroknak és oszlopoknak nevezzük.
E definíció szerint egy A mátrixnak több bázismollja is lehet.
Az E identitásmátrix rangja n (a sorok száma).
1. példa Adott két mátrix, és kiskorúaik 
, 
. Ezek közül melyik tekinthető alapnak?
Megoldás. Minor M 1 =0, tehát nem lehet alapja egyik mátrixnak sem. Minor M 2 =-9≠0, és 2-es rendű, ami azt jelenti, hogy az A vagy / és B mátrixok alapjaként vehetők igénybe, feltéve, hogy rangjuk 2-vel egyenlő. Mivel detB=0 (determinánsként két arányos oszloppal), ezért rangB=2 és M 2 vehető a B mátrix alapmolljának. Az A mátrix rangja 3, amiatt, hogy detA=-27≠ 0, és ezért ennek a mátrixnak a bázis-moll sorrendjének 3-nak kell lennie, azaz M 2 nem alapja az A mátrixnak. Vegye figyelembe, hogy az A mátrixnak egyetlen bázis-mollja van, amely megegyezik az A mátrix determinánsával.
Tétel (az alap-mollról).
A mátrix bármely sora (oszlopa) az alapsorok (oszlopok) lineáris kombinációja.
Következmények a tételből.
2. példa Keresse meg a mátrix rangját 
.
Megoldás.
A mátrix rang definíciója alapján a legmagasabb rendű, nullától eltérő mollot fogunk keresni. Először átalakítjuk a mátrixot többre egyszerű nézet. Ehhez szorozzuk meg a mátrix első sorát (-2)-vel, és adjuk hozzá a másodikhoz, majd szorozzuk (-1)-gyel és adjuk hozzá a harmadikhoz.
A mátrixrang fogalmának használatához információra lesz szükségünk az "Algebrai komplementerek és mollok. A moll típusok és az algebrai kiegészítések" témakörből. Mindenekelőtt ez a „matrix minor” kifejezésre vonatkozik, mivel a mátrix rangját pontosan a minorokon keresztül határozzuk meg.
Mátrix rang a kiskorúak maximális sorrendje, amelyek között van legalább egy, amely nem egyenlő nullával.
Egyenértékű mátrixok- mátrixok, amelyek rangjai egyenlőek egymással.
Hadd magyarázzuk el részletesebben. Tegyük fel, hogy a másodrendű kiskorúak között van legalább egy nullától eltérő. És minden kiskorú, akinek a sorrendje kettőnél magasabb, egyenlő nullával. Következtetés: a mátrix rangja 2. Vagy például a tizedik rendű kiskorúak között van legalább olyan, amelyik nem egyenlő nullával. És minden kiskorú, akinek a sorrendje nagyobb, mint 10, egyenlő nullával. Következtetés: a mátrix rangja 10.
A $A$ mátrix rangját a következőképpen jelöljük: $\rang A$ vagy $r(A)$. A nulla $O$ mátrix rangja nullának számít, $\rang O=0$. Hadd emlékeztesselek arra, hogy egy mátrix-moll létrehozásához sorokat és oszlopokat kell áthúzni, de lehetetlen több sort és oszlopot áthúzni, mint amennyit maga a mátrix tartalmaz. Például, ha a $F$ mátrix mérete $5\x 4$ (azaz 5 sort és 4 oszlopot tartalmaz), akkor a kisebbek maximális sorrendje négy. A továbbiakban nem lehet ötödrendű kiskorúakat képezni, mivel ezekhez 5 oszlopra lesz szükség (és nekünk csak 4). Ez azt jelenti, hogy a $F$ mátrix rangja nem lehet több négynél, azaz. $\rang F≤4$.
Általánosabb formában a fentiek azt jelentik, hogy ha egy mátrix $m$ sort és $n$ oszlopot tartalmaz, akkor a rangja nem haladhatja meg a $m$ és $n$ közül a legkisebbet, azaz. $\rang A≤\min(m,n)$.
Elvileg már a rang meghatározásából következik a megtalálásának módszere. A mátrix rangjának meghatározásának folyamata definíció szerint sematikusan a következőképpen ábrázolható:
Hadd magyarázzam el ezt a diagramot részletesebben. Kezdjük az okoskodást a legelején, azaz. valamilyen $A$ mátrix elsőrendű minorjaiból.
Mi vár ránk ennek az eljárásnak a végén? Előfordulhat, hogy a k-edik rendű kiskorúak között lesz legalább egy nullától eltérő, és minden (k+1) rendű kiskorú nullával egyenlő. Ez azt jelenti, hogy k a kiskorúak maximális sorrendje, amelyek között van legalább olyan, amelyik nem egyenlő nullával, azaz. a rang egyenlő lesz k-val. Előfordulhat más helyzet is: a k-rendű kiskorúak között lesz legalább olyan, amelyik nem egyenlő nullával, de (k+1) rendű kiskorúak képzése már nem lehetséges. Ebben az esetben a mátrix rangja is egyenlő k-val. Röviden, az utoljára megkomponált nem nulla moll sorrendje lesz ranggal egyenlő mátrixok.
Térjünk át a példákra, amelyekben a mátrix rangjának meghatározásának folyamata definíció szerint világosan bemutatásra kerül. Hadd hangsúlyozzam még egyszer, hogy a téma példáiban a mátrixok rangját csak a rang definíciójával találjuk meg. Az egyéb módszereket (mátrix rangjának kiszámítása kiskorúak határolásának módszerével, mátrix rangjának kiszámítása elemi transzformációk módszerével) a következő témakörökben tárgyaljuk.
Egyébként egyáltalán nem szükséges a legkisebb rendű kiskorúakkal megkezdeni a besorolási eljárást, ahogy az az 1. és 2. számú példákban történt. Azonnal áttérhet a magasabb rendű kiskorúakra (lásd a 3. példát).
1. számú példa
Keresse meg a mátrix rangját $A=\left(\begin(array)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(array) \right)$.
Ennek a mátrixnak a mérete $3\x5$, azaz. három sort és öt oszlopot tartalmaz. A 3-as és 5-ös számok közül a minimum 3, ezért a $A$ mátrix rangja nem több 3-nál, azaz. $\rang A≤ 3$. És ez az egyenlőtlenség nyilvánvaló, hiszen már nem tudunk negyedrendű kiskorúakat képezni - ezekhez 4 sor szükséges, nekünk pedig csak 3. Térjünk át közvetlenül az adott mátrix rangjának meghatározására.
Az elsőrendű kiskorúak között (azaz a $A$ mátrix elemei között) vannak a nullától eltérő egyek. Például 5, -3, 2, 7. Általában nem érdekel bennünket a nullától eltérő elemek száma. Van legalább egy nem nulla elem – és ez elég. Mivel az elsőrendű kiskorúak között van legalább egy nullától eltérő, azt a következtetést vonjuk le, hogy $\rang A≥ 1$, és folytassuk a másodrendű kiskorúak ellenőrzését.
Kezdjük a másodrendű kiskorúak felfedezését. Például az 1., 2. sorok és az 1. és 4. oszlopok metszéspontjában a következő mellékelemek találhatók: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right| $. Ennél a determinánsnál a második oszlop minden eleme nulla, ezért maga a determináns is egyenlő nullával, azaz. $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=0$ (lásd a 3. tulajdonságot a determinánsok tulajdonságai témakörben). Vagy egyszerűen kiszámíthatja ezt a determinánst a másod- és harmadrendű determinánsok kiszámítása című rész 1. képletével:
$$ \left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=5\cdot 0-0\cdot 7=0. $$
Az általunk tesztelt első másodrendű moll nullával egyenlő. Mit is jelent ez? A másodrendű kiskorúak további ellenőrzésének szükségességéről. Vagy mindegyik nulla lesz (és akkor a rang egyenlő lesz 1-gyel), vagy lesz köztük legalább egy kisebb, amely különbözik a nullától. Próbáljunk meg jobb választást hozni egy másodrendű minor írásával, melynek elemei az 1., 2. sorok és az 1. és 5. számú oszlopok metszéspontjában helyezkednek el: $\left|\begin( tömb)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|$. Keressük ennek a másodrendű minornak az értékét:
$$ \left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|=5\cdot 3-2\cdot 7=1. $$
Ez a moll nem egyenlő nullával. Következtetés: a másodrendű kiskorúak között van legalább egy nullától eltérő. Ezért $\rang A≥ 2$. Tovább kell lépnünk a harmadrendű kiskorúak tanulmányozására.
Ha a 2-es vagy a 4-es oszlopot választjuk harmadrendű kiskorúak képzéséhez, akkor ezek a minorok nullával egyenlőek (mivel nulla oszlopot tartalmaznak). Már csak egy harmadrendű minor ellenőrzése van hátra, amelynek elemei az 1., 3., 5. számú oszlopok és az 1., 2., 3. sorok metszéspontjában helyezkednek el. Jegyezzük fel ezt a kisebbet, és keressük meg az értékét:
$$ \left|\begin(array)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(array) \right|=-20-18-14 +16+21+15=0. $$
Tehát minden harmadrendű kiskorú egyenlő nullával. Az általunk összeállított utolsó nem nulla moll másodrendű volt. Következtetés: a kiskorúak maximális sorrendje, amelyek között van legalább egy nem nulla, 2. Ezért $\rang A=2$.
Válasz: $\rang A=2$.
2. példa
Keresse meg a mátrix rangját $A=\left(\begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 & 7 & 8 & -7 \end(array) \right)$.
Nekünk van négyzetmátrix negyedik rend. Rögtön megjegyezzük, hogy ennek a mátrixnak a rangja nem haladja meg a 4-et, azaz. $\rang A≤ 4$. Kezdjük el megkeresni a mátrix rangját.
Az elsőrendű minorok között (azaz a $A$ mátrix elemei között) van legalább olyan, amelyik nem egyenlő nullával, ezért $\rang A≥ 1$. Térjünk át a másodrendű kiskorúak ellenőrzésére. Például a 2., 3. sorok, valamint az 1. és 2. oszlopok metszéspontjában a következő másodrendű melléket kapjuk: $\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|$. Számítsuk ki:
$$\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|=0-10=-10. $$
A másodrendű kiskorúak között van legalább olyan, amelyik nem egyenlő nullával, tehát $\rang A≥ 2$.
Térjünk át a harmadrendű kiskorúakra. Keressünk például egy kisebbet, amelynek elemei az 1., 3., 4. sorok és az 1., 2., 4. számú oszlopok metszéspontjában helyezkednek el:
$$\left | \begin(tömb) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(tömb) \right|=105-105=0. $$
Mivel ez a harmadrendű kiskorú nullával egyenlő, egy másik harmadrendű kiskorú vizsgálatára van szükség. Vagy mindegyik egyenlő nullával (akkor a rang 2 lesz), vagy lesz köztük legalább egy, amely nem egyenlő nullával (akkor kezdjük el a negyedrendű kiskorúak tanulmányozását). Tekintsünk egy harmadrendű minort, melynek elemei a 2., 3., 4. sorok és a 2., 3., 4. számú oszlopok metszéspontjában helyezkednek el:
$$\left| \begin(tömb) (cccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(tömb) \right|=-28. $$
A harmadrendű kiskorúak között van legalább egy nullától eltérő, tehát $\rang A≥ 3$. Térjünk át a negyedrendű kiskorúak ellenőrzésére.
Bármely negyedrendű minor a $A$ mátrix négy sorának és négy oszlopának metszéspontjában található. Más szóval, a negyedrendű moll a $A$ mátrix determinánsa, mivel ez a mátrix 4 sort és 4 oszlopot tartalmaz. Ennek a mátrixnak a determinánsát a "A determináns sorrendjének csökkentése. A determináns sorban (oszlopban) történő felbontása" című témakör 2. példájában számítottuk ki, tehát vegyük csak a kész eredményt:
$$\left| \begin(tömb) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (tömb)\jobbra|=86. $$
Tehát a negyedrendű moll nem egyenlő nullával. Ötödrendű kiskorúakat már nem képezhetünk. Következtetés: a kiskorúak legmagasabb sorrendje, amelyek között van legalább egy nem nulla, 4. Eredmény: $\rang A=4$.
Válasz: $\rang A=4$.
3. példa
Keresse meg a mátrix rangját $A=\left(\begin(array) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( array) \right)$.
Rögtön megjegyezzük, hogy ez a mátrix 3 sort és 4 oszlopot tartalmaz, tehát $\rang A≤ 3$. Az előző példákban a rang megállapításának folyamatát a legkisebb (első) rendű kiskorúak figyelembevételével kezdtük. Itt igyekszünk a lehető legmagasabb rendű kiskorúakat azonnal ellenőrizni. A $A$ mátrix esetében ezek a harmadrendű kiskorúak. Tekintsünk egy harmadrendű minort, amelynek elemei az 1., 2., 3. sorok és a 2., 3., 4. oszlopok metszéspontjában helyezkednek el:
$$\left| \begin(array) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(array) \right|=-8-60-20=-88. $$
Tehát a kiskorúak legmagasabb rendje, amelyek között van legalább egy, amely nem egyenlő nullával, a 3. Ezért a mátrix rangja 3, azaz. $\rang A=3$.
Válasz: $\rang A=3$.
Általánosságban elmondható, hogy egy mátrix rangjának meghatározása definíció szerint a következő általános eset a feladat meglehetősen munkaigényes. Például egy viszonylag kis, $5\x4$ méretű mátrixban 60 másodrendű kiskorú van. És még ha ezek közül 59 egyenlő nullával, akkor a 60. moll nem nulla lehet. Ezután harmadrendű kiskorúakat kell tanulnod, amiből ez a mátrix 40 darabot tartalmaz. Általában kevésbé körülményes módszereket próbálnak alkalmazni, mint például a kiskorúak határolásának módszere vagy az azzal egyenértékű átalakítások módszere.
Adjunk meg néhány mátrixot:
.
Ebben a mátrixban válasszunk 
tetszőleges karakterláncok és 
tetszőleges oszlopok 
. Aztán a meghatározó 
rendű, mátrixelemekből áll 
, amely a kiválasztott sorok és oszlopok metszéspontjában található, melléknévnek nevezzük 
rendű mátrix 
.
Meghatározás 1.13. Mátrix rang 
ennek a mátrixnak a nem nulla moll legnagyobb rendje.
Egy mátrix rangjának kiszámításához figyelembe kell venni annak összes legalacsonyabb rendű minorját, és ha legalább az egyik nullától eltérő, akkor folytassa a legmagasabb rendű minorok figyelembevételével. A mátrix rangjának meghatározásának ezt a megközelítését határolási módszernek (vagy kiskorúak határolásának módszerének) nevezik.
Probléma 1.4. A kiskorúak határolásának módszerével határozzuk meg a mátrix rangját! 
.
.
Vegyük például az elsőrendű szegélyezést, 
. Ezután áttérünk néhány másodrendű szegélyre.
Például, 
.
Végül elemezzük a harmadrendű határvonalat.
.
Tehát a nem nulla moll legmagasabb rendje 2, tehát 
.
Az 1.4. feladat megoldása során észrevehető, hogy számos másodrendű határos kiskorú nem nulla. E tekintetben a következő koncepció érvényes.
Meghatározás 1.14. A mátrix bázismollja minden nullától eltérő moll, amelynek sorrendje megegyezik a mátrix rangjával.
Tétel 1.2.(Alap-moll tétel). Az alapsorok (bázisoszlopok) lineárisan függetlenek.
Vegyük észre, hogy egy mátrix sorai (oszlopai) akkor és csak akkor lineárisan függőek, ha legalább az egyik a többi lineáris kombinációjaként ábrázolható.
Tétel 1.3. A lineárisan független mátrixsorok száma megegyezik a lineárisan független mátrixoszlopok számával, és egyenlő a mátrix rangjával.
Tétel 1.4.(Szükséges és elégséges feltétel, hogy a determináns nullával egyenlő legyen). Annak érdekében, hogy a meghatározó 
-edik sorrend 
nullával egyenlő volt, szükséges és elegendő, hogy sorai (oszlopai) lineárisan függőek legyenek.
Egy mátrix rangjának kiszámítása a definíciója alapján túlságosan körülményes. Ez különösen fontos a magas rendű mátrixok esetében. Ebben a tekintetben a gyakorlatban a mátrix rangját a 10.2 - 10.4 tételek alkalmazása, valamint a mátrix ekvivalencia és az elemi transzformációk alkalmazása alapján számítják ki.
Meghatározás 1.15. Két mátrix 
És 
ekvivalensnek nevezzük, ha a rangjuk egyenlő, azaz. 
.
Ha mátrixok 
És 
egyenértékűek, akkor vegye figyelembe 
.
Tétel 1.5. A mátrix rangja az elemi transzformációk miatt nem változik.
Elemi mátrix transzformációnak nevezzük 
a következő műveletek bármelyike egy mátrixon:
Sorok cseréje oszlopokkal és oszlopok cseréje megfelelő sorokkal;
Mátrix sorok átrendezése;
Egy olyan vonal áthúzása, amelynek minden eleme nulla;
Egy karakterlánc szorzása nullától eltérő számmal;
Egy sor elemeihez hozzáadva egy másik sor megfelelő elemeit, megszorozva ugyanazzal a számmal 
.
Az 1.5. tétel következménye. Ha mátrix 
mátrixból nyerjük 
véges számú elemi transzformáció segítségével, akkor a mátrix 
És 
egyenértékűek.
Egy mátrix rangjának számításakor véges számú elemi transzformáció segítségével trapéz alakúra kell redukálni.
Meghatározás 1.16. Trapéznek nevezzük a mátrix olyan ábrázolási formáját, amikor a határos mollban van a legmagasabb magasabb rendű nem nulla, az átlósok alatti összes elem nullává válik. Például:
.
Itt 
, mátrixelemek 
menj a nullára. Ekkor egy ilyen mátrix ábrázolási formája trapéz alakú lesz.
A mátrixokat általában trapéz alakúra redukáljuk a Gauss-algoritmus segítségével. A Gauss-algoritmus lényege, hogy a mátrix első sorának elemeit a megfelelő tényezőkkel megszorozva elérjük, hogy az első oszlop minden eleme az elem alatt helyezkedik el. 
, nullára fordulna. Ezután megszorozva a második oszlop elemeit a megfelelő tényezőkkel, biztosítjuk, hogy a második oszlop minden eleme az elem alatt helyezkedik el. 
, nullára fordulna. Ezután járjon el ugyanúgy.
Probléma 1.5. Határozza meg a mátrix rangját trapéz alakúra redukálva.
.
A Gauss-algoritmus használatának megkönnyítése érdekében felcserélheti az első és a harmadik sort.
.
Nyilvánvaló, hogy itt 
. Azonban, hogy az eredmény elegánsabb formát hozzon, folytathatja az oszlopok átalakítását.
.
Meghatározás. Mátrix rang a vektornak tekintett lineárisan független sorok maximális száma.
1. tétel a mátrix rangjáról. Mátrix rang egy mátrix nullától eltérő moll maximális rendjének nevezzük.
A kiskorú fogalmát a meghatározó tényezőkről szóló leckében már tárgyaltuk, most pedig általánosítjuk. Vegyünk egy bizonyos számú sort és bizonyos számú oszlopot a mátrixban, és ez a „mennyi” legyen kevesebb, mint a mátrix sorainak és oszlopainak száma, sorok és oszlopok esetén pedig ez a „hány” legyen a ugyanaz a szám. Ekkor a hány sor és hány oszlop metszéspontjában lesz az eredeti mátrixunknál alacsonyabb rendű mátrix. A determináns egy mátrix, és k-edik rendű minor lesz, ha az említett „néhányat” (a sorok és oszlopok számát) k-val jelöljük.
Meghatározás. Kisebb ( r+1) sorrend, amelyen belül a kiválasztott kiskorú fekszik r-edik rendet határolásnak nevezzük adott kiskorú esetében.
A két leggyakrabban használt módszer a a mátrix rangjának megtalálása. Ez kiskorúakkal való határolás módjaÉs elemi transzformációk módszere(Gauss-módszer).
A bordering minors módszer alkalmazásakor a következő tételt használjuk.
2. tétel a mátrix rangjáról. Ha egy moll mátrixelemekből összeállítható r sorrendben, nem egyenlő nullával, akkor a mátrix rangja egyenlő r.
Az elemi átalakítási módszer használatakor a következő tulajdonságot használjuk:
Ha elemi transzformációkkal olyan trapézmátrixot kapunk, amely egyenértékű az eredetivel, akkor ennek a mátrixnak a rangja a benne lévő sorok száma, kivéve azokat a sorokat, amelyek teljes egészében nullákból állnak.
Befoglaló kiskorú az adotthoz képest magasabb rendű kiskorú, ha ez a magasabb rendű kiskorú tartalmazza az adott kiskorút.
Például adott a mátrix
Vegyünk egy kiskorút
A szomszédos kiskorúak lesznek:
Algoritmus egy mátrix rangjának meghatározására következő.
1. Keressen másodrendű kisebbeket, amelyek nem egyenlők nullával! Ha minden másodrendű minor nulla, akkor a mátrix rangja eggyel lesz egyenlő ( r =1 ).
2. Ha van legalább egy másodrendű moll, amely nem egyenlő nullával, akkor összeállítjuk a harmadrendű határoló mollokat. Ha az összes határos harmadrendű kiskorú nulla, akkor a mátrix rangja egyenlő kettővel ( r =2 ).
3. Ha a harmadrendű határos kiskorúak közül legalább egy nem egyenlő nullával, akkor összeállítjuk a határos kiskorúakat. Ha a negyedrendű összes határos kiskorú nulla, akkor a mátrix rangja egyenlő hárommal ( r =2 ).
4. Folytassa így, amíg a mátrix mérete megengedi.
1. példa Keresse meg a mátrix rangját
.
Megoldás. Másodrendű minor 
.
Határozzuk meg. Négy szomszédos kiskorú lesz:
,
,
Így minden harmadik rendű szomszédos kiskorú nulla, ezért ennek a mátrixnak a rangja egyenlő kettővel ( r =2 ).
2. példa Keresse meg a mátrix rangját
Megoldás. Ennek a mátrixnak a rangja egyenlő 1-gyel, mivel ennek a mátrixnak minden másodrendű kiskorúja nulla (ebben, mint a következő két példában a szomszédos kiskorúak esetében, kérjük a kedves hallgatókat, hogy ellenőrizzék, önmagukat, esetleg a determinánsok kiszámításának szabályait alkalmazva), és az elsőrendű minorok között, azaz a mátrix elemei között vannak nem nullák.
3. példa Keresse meg a mátrix rangját
Megoldás. Ennek a mátrixnak a másodrendű mollja, és ennek a mátrixnak minden harmadrendű mollja egyenlő nullával. Ezért ennek a mátrixnak a rangja kettő.
4. példa Keresse meg a mátrix rangját
Megoldás. Ennek a mátrixnak a rangja 3, mivel ennek a mátrixnak az egyetlen harmadrendű mollja a 3.
Már az 1. példában is jól látható, hogy a kiskorúak határos módszerével egy mátrix rangjának meghatározásához nagyszámú determináns számítása szükséges. Van azonban mód arra, hogy a számítási mennyiséget minimálisra csökkentsük. Ez a módszer elemi mátrix transzformációk használatán alapul, és Gauss-módszernek is nevezik.
A következő műveletek elemi mátrix transzformációnak minősülnek:
1) a mátrix bármely sorát vagy oszlopát megszorozzuk nullától eltérő számmal;
2) a mátrix bármely sorának vagy oszlopának elemeihez hozzáadjuk egy másik sor vagy oszlop megfelelő elemeit, szorozva ugyanazzal a számmal;
3) a mátrix két sorának vagy oszlopának felcserélése;
4) a „null” sorok eltávolítása, vagyis azok, amelyek elemei nullával egyenlők;
5) az összes arányos vonal törlése egy kivételével.
Tétel. Egy elemi transzformáció során a mátrix rangja nem változik. Más szóval, ha elemi transzformációkat használunk a mátrixból A a mátrixhoz ment B, Azt .
Megfontoljuk a téma egy fontos gyakorlati alkalmazását is: rendszerkutatás lineáris egyenletek az összetartozásért.
A cikk humoros epigráfiája nagy mennyiségű igazságot tartalmaz. A „rang” szót általában valamilyen hierarchiához kötjük, leggyakrabban egy karrierlétrához. Minél több tudással, tapasztalattal, képességekkel, kapcsolatokkal, stb. – minél magasabb pozíciója és lehetőségei közé tartozik. Ifjúsági értelemben a rang a „meredekség” általános fokára utal.
Matematikus testvéreink pedig ugyanezen elvek szerint élnek. Vegyünk néhány véletlenszerűt sétálni nulla mátrixok:
Gondoljunk bele, ha a mátrixban csupa nulla, akkor milyen rangról beszélhetünk? Mindenki ismeri a „teljes nulla” informális kifejezést. A mátrixok társadalmában minden pontosan ugyanaz:
A nulla mátrix rangjabármely méret nulla.
jegyzet : A nulla mátrixot a görög "théta" betű jelöli
A mátrix rangjának jobb megértése érdekében a továbbiakban anyagokat használok segítségül analitikus geometria. Tekintsük nullát vektor a miénk háromdimenziós tér, amely nem határoz meg konkrét irányt és használhatatlan az építkezéshez affin alapon. Algebrai szempontból ennek a vektornak a koordinátái be vannak írva mátrix„egyenként” és logikus (a jelzett geometriai értelemben) Tegyük fel, hogy ennek a mátrixnak a rangja nulla.
Most nézzünk meg néhányat nem nulla oszlopvektorokÉs sorvektorok:
Minden példánynak van legalább egy nullától eltérő eleme, és ez már valami!
Bármely nem nulla sorvektor (oszlopvektor) rangja eggyel egyenlő
És általában véve - ha a mátrixban tetszőleges méretek van legalább egy nem nulla elem, akkor a rangja nem kevesebb egységek.
Az algebrai sorvektorok és oszlopvektorok bizonyos mértékig absztraktak, ezért térjünk vissza a geometriai asszociációra. Nem nulla vektor nagyon határozott irányt szab a térben és alkalmas a konstrukcióra alapján, ezért a mátrix rangját eggyel egyenlőnek tekintjük.
Elméleti információk : a lineáris algebrában a vektor egy (8 axiómával meghatározott) vektortér eleme, amely különösen lehet valós számok rendezett sora (vagy oszlopa) a hozzájuk meghatározott összeadás és szorzás műveletekkel. valós szám. Többel részletes információk a vektorokról a cikkben olvashat Lineáris transzformációk.
lineárisan függő(egymáson keresztül kifejezve). Geometriai szempontból a második sor a kollineáris vektor koordinátáit tartalmazza 
, ami egyáltalán nem vitte előre az ügyet az építésben háromdimenziós alapon, lévén ebben az értelemben felesleges. Így ennek a mátrixnak a rangja is egyenlő eggyel.
Írjuk át a vektorok koordinátáit oszlopokba ( transzponálja a mátrixot):
Mi változott a rangot tekintve? Semmi. Az oszlopok arányosak, ami azt jelenti, hogy a rang egyenlő eggyel. Egyébként vegye figyelembe, hogy mindhárom sor arányos is. A koordinátákkal azonosíthatók három a sík kollineáris vektorai, amelyek közül csak egy"lapos" alap felépítéséhez hasznos. És ez teljes mértékben összhangban van geometriai rangérzetünkkel.
A fenti példából egy fontos megállapítás következik:
A sorokban a mátrix rangja megegyezik a mátrix oszlopos rangjával. Ezt már említettem egy kicsit a hatékony leckében a determináns kiszámításának módszerei.
jegyzet : a sorok lineáris függése az oszlopok lineáris függését jelenti (és fordítva). De az idő megtakarítása érdekében és megszokásból szinte mindig a húrok lineáris függőségéről fogok beszélni.
Folytassuk szeretett házi kedvencünk képzését. Adjuk hozzá egy másik kollineáris vektor koordinátáit a harmadik sorban lévő mátrixhoz 
:
Segített nekünk egy háromdimenziós alap felépítésében? Természetesen nem. Mindhárom vektor ugyanazon az úton jár oda-vissza, és a mátrix rangja eggyel egyenlő. Tetszőleges számú kollineáris vektort vehetsz, mondjuk 100-at, koordinátáikat egy „százszor három” mátrixba teheted, és egy ilyen felhőkarcoló rangja továbbra is egy marad.
Ismerkedjünk meg a mátrixszal, melynek sorai lineárisan független. Egy nem-kollineáris vektorpár alkalmas háromdimenziós bázis felépítésére. Ennek a mátrixnak a rangja kettő.
Mi a mátrix rangja? Úgy tűnik, hogy a vonalak nem arányosak... szóval elméletben három. Ennek a mátrixnak a rangja azonban szintén kettő. Az első két sort hozzáadtam, és az eredményt alul írtam, i.e. lineárisan kifejezve a harmadik sor az első kettőn keresztül. Geometriailag a mátrix sorai három koordinátájának felelnek meg koplanáris vektorok, és e három között van egy pár nem kollineáris elvtárs.
Amint látod, lineáris függőség a figyelembe vett mátrixban nem nyilvánvaló, és ma megtanuljuk, hogyan hozzuk ki a szabadba.
Szerintem sokan kitalálják, mi a mátrix rangja!
Tekintsünk egy mátrixot, amelynek sorai lineárisan független. Vektorok alkotnak affin alapon, és ennek a mátrixnak a rangja három.
Mint tudják, a háromdimenziós tér bármely negyedik, ötödik, tizedik vektorát lineárisan fejezzük ki bázisvektorokkal. Ezért ha tetszőleges számú sort ad hozzá egy mátrixhoz, akkor a rangja akkor is egyenlő lesz hárommal.
Hasonló érvelés végezhető mátrixokkal is nagyobb méretek(természetesen minden geometriai jelentés nélkül).
Meghatározás : A mátrix rangja a lineárisan független sorok maximális száma. Vagy: A mátrix rangja a lineárisan független oszlopok maximális száma. Igen, a számuk mindig ugyanaz.
A fentiekből egy fontos gyakorlati útmutató is következik: a mátrix rangja nem haladja meg annak minimális méretét. Például a mátrixban 
négy sor és öt oszlop. A minimális méret négy, ezért ennek a mátrixnak a rangja biztosan nem haladja meg a 4-et.
Megnevezések: a világelméletben és a gyakorlatban nincs általánosan elfogadott szabvány a mátrix rangjának meghatározására, leggyakrabban a következőket találhatja: - ahogy mondani szokás, az angol egyet ír, a német mást. Ezért az amerikai és orosz pokolról szóló híres vicc alapján jelöljük a mátrix rangját anyaszóval. Például: . És ha a mátrix „névtelen”, amelyből sok van, akkor egyszerűen írhat .
Ha a nagymamámnak egy ötödik oszlopa lenne a mátrixában, akkor egy másik 4. rendű kiskorút kellene kiszámolnia ("kék", "málna" + 5. oszlop).
Következtetés: a nullától eltérő moll maximális sorrendje három, ami azt jelenti.
Talán még nem értettek meg mindent teljesen ezt a kifejezést: a 4. rendű moll egyenlő nullával, de a 3. rendű mollok között volt egy nullától eltérő egy - ezért a maximális rend nem nulla kisebb és egyenlő hárommal.
Felmerül a kérdés, miért nem számítjuk ki azonnal a determinánst? Nos, először is, a legtöbb feladatban a mátrix nem négyzet alakú, másodszor, még ha nullától eltérő értéket is kap, a feladat valószínűleg elutasításra kerül, mivel általában szabványos „alulról felfelé” történő megoldást tartalmaz. És a vizsgált példában a 4. sorrend nulla determinánsa lehetővé teszi, hogy kijelentsük, hogy a mátrix rangja csak négynél kisebb.
Bevallom, a saját magam által elemzett problémát azért találtam ki, hogy jobban elmagyarázzam a kiskorúak határolásának módszerét. A gyakorlatban minden egyszerűbb:
2. példa
Keresse meg a mátrix rangját az él minors módszerrel 
A megoldás és a válasz a lecke végén található.
Mikor működik a leggyorsabban az algoritmus? Térjünk vissza ugyanahhoz a négyszer négyes mátrixhoz. 
. Nyilván a „jó” esetén lesz a legrövidebb a megoldás sarki kiskorúak: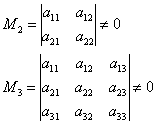
És ha , akkor , különben – .
A gondolkodás egyáltalán nem hipotetikus – számos példa van arra, hogy az egész ügy csak szögletes kiskorúakra korlátozódik.
Bizonyos esetekben azonban egy másik módszer hatékonyabb és előnyösebb:
A bekezdés azoknak az olvasóknak szól, akik már ismerik Gauss-módszerés többé-kevésbé a kezükbe került.
Technikai szempontból a módszer nem újszerű:
1) elemi transzformációk segítségével a mátrixot lépcsőzetes formára redukáljuk;
2) a mátrix rangja megegyezik a sorok számával.
Ez teljesen egyértelmű a Gauss-módszer használata nem változtatja meg a mátrix rangját, és a lényeg itt rendkívül egyszerű: az algoritmus szerint az elemi átalakítások során minden szükségtelen arányos (lineárisan függő) sort azonosítanak és eltávolítanak, ami egy „száraz maradékot” eredményez - a lineárisan független sorok maximális számát.
Alakítsuk át a régi ismert mátrixot három kollineáris vektor koordinátáival: 
(1) Az első sort hozzáadtuk a másodikhoz, megszorozva –2-vel. Az első sort hozzáadtuk a harmadikhoz.
(2) A nulla vonalakat eltávolítják.
Így egy sor maradt, tehát . Mondanom sem kell, hogy ez sokkal gyorsabb, mint kilenc nulla 2. rendű mollot kiszámítani, és csak azután levonni a következtetést.
Emlékeztetlek erre önmagában algebrai mátrix semmit nem lehet megváltoztatni, és az átalakításokat csak a rang megállapítása céljából végezzük! Apropó, időzzünk még egyszer a kérdésnél, hogy miért ne? Forrásmátrix 
olyan információt hordoz, amely alapvetően különbözik a mátrix és a sor információitól. Néhány matematikai modellek(nem túlzás) az egy szám különbsége létkérdés lehet. ...Eszembe jutottak az általános és középiskolai matematikatanárok, akik kíméletlenül 1-2 ponttal csökkentették az osztályzatokat a legkisebb pontatlanság vagy az algoritmustól való eltérés miatt. És rettenetesen kiábrándító volt, amikor a garantáltnak tűnő „A” helyett „jó” vagy még rosszabb lett. Sokkal később jött a megértés – hogyan lehetne másként műholdakat, nukleáris robbanófejeket és erőműveket egy emberre bízni? De ne aggódj, én nem dolgozom ezeken a területeken =)
Térjünk át az értelmesebb feladatokra, ahol többek között fontos számítási technikákkal ismerkedünk meg Gauss módszer:
3. példa
Keresse meg a mátrix rangját elemi transzformációk segítségével 
Megoldás: egy „négyszer öt” mátrix van megadva, ami azt jelenti, hogy a rangja biztosan nem több 4-nél.
Az első oszlopban nincs 1 vagy –1, ezért további műveletekre van szükség legalább egy egység megszerzéséhez. Az oldal fennállása során többször is feltették velem a kérdést: „Lehetséges-e az oszlopok átrendezése elemi átalakítások során?” Itt átrendeztük az első és a második oszlopot, és minden rendben! A legtöbb olyan feladatban, ahol használják Gauss-módszer, az oszlopok valóban átrendezhetők. DE NEM SZÜKSÉGES. És a lényeg nem is a változókkal való esetleges összekeverésben van, hanem az, hogy a klasszikus tanmenetben felsőbb matematika ezt az akciót hagyományosan nem veszik számításba, így egy ilyen hitványt NAGYON ferdén fognak nézni (vagy akár mindent újra kell csinálni).
A második pont a számokra vonatkozik. A döntés meghozatalakor hasznos a következő ökölszabály alkalmazása: az elemi transzformációk lehetőleg csökkentsék a mátrixszámokat. Végül is sokkal könnyebb eggyel, kettővel, hárommal dolgozni, mint például a 23-mal, 45-tel és 97-tel. És az első akció nem csak az első oszlopban szereplő egyes megszerzésére irányul, hanem a számok kiiktatására is. 7 és 11.
Először a teljes megoldás, majd a megjegyzések: 
(1) Az első sort hozzáadtuk a másodikhoz, megszorozva –2-vel. Az első sort hozzáadtuk a harmadikhoz, megszorozva –3-mal. És a kupachoz: az 1. sort hozzáadtuk a 4. sorhoz, megszorozva -1-gyel.
(2) Az utolsó három sor arányos. A 3. és 4. sor kikerült, a második sor az első helyre került.
(3) Az első sort hozzáadtuk a másodikhoz, megszorozva –3-mal.
A lépcsős formára redukált mátrixnak két sora van.
Válasz:
Most rajtad a sor, hogy megkínozza a négyszer négyes mátrixot:
4. példa
Keresse meg a mátrix rangját a Gauss-módszerrel 
emlékeztetlek erre Gauss-módszer nem utal egyértelmű merevségre, és az Ön döntése nagy valószínűséggel eltér az én döntésemtől. Rövid példa egy feladatra a lecke végén.
A gyakorlatban sokszor egyáltalán nincs megmondva, hogy milyen módszerrel kell a rangot megállapítani. Ilyen helyzetben elemezni kell a feltételt - egyes mátrixok esetében ésszerűbb a kiskorúak megoldása, míg mások számára sokkal jövedelmezőbb az elemi transzformációk alkalmazása:
5. példa
Keresse meg a mátrix rangját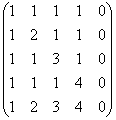 
Megoldás: az első módszer valahogy azonnal eltűnik =)
Kicsit feljebb azt tanácsoltam, hogy ne érintsd meg a mátrix oszlopait, de ha nulla oszlop van, vagy arányos/egybeeső oszlopok, akkor is érdemes amputálni: 
(1) Az ötödik oszlop nulla, távolítsa el a mátrixból. Így a mátrix rangja nem több, mint négy. Az első sort –1-gyel szoroztuk. Ez a Gauss-módszer másik jellegzetessége, amely a következő műveletet kellemes sétává varázsolja:
(2) A másodiktól kezdve minden sorhoz hozzáadtuk az első sort.
(3) Az első sort –1-gyel szoroztuk, a harmadikat 2-vel, a negyediket 3-mal. A második sort hozzáadtuk az ötödikhez, megszorozva –1-gyel.
(4) A harmadik sort hozzáadtuk az ötödikhez, megszorozva –2-vel.
(5) Az utolsó két sor arányos, az ötödik törlésre kerül.
Az eredmény 4 sor.
Válasz:
Szabványos ötszintes épület független tanulmányozáshoz:
6. példa
Keresse meg a mátrix rangját
Rövid megoldás és válasz a lecke végén.
Meg kell jegyezni, hogy a „mátrix rang” kifejezést nem látják olyan gyakran a gyakorlatban, és a legtöbb problémában teljesen nélkülözheti. De van egy feladat, ahol a kérdéses fogalom a fő színész, és a cikk befejezéseként megvizsgáljuk ezt a gyakorlati alkalmazást:
Gyakran a megoldás mellett lineáris egyenletrendszerek a feltétel szerint először meg kell vizsgálni a kompatibilitást, vagyis annak bizonyítását, hogy egyáltalán létezik-e megoldás. Az ilyen ellenőrzésben kulcsszerepet játszik Kronecker-Capelli tétel, amit a szükséges formában megfogalmazok:
Ha rang rendszermátrixok ranggal egyenlő kiterjesztett mátrix rendszer, akkor a rendszer konzisztens, és ha ez a szám egybeesik az ismeretlenek számával, akkor a megoldás egyedi.
Így a rendszer kompatibilitási vizsgálatához ellenőrizni kell az egyenlőséget 
, Ahol - rendszermátrix(emlékezz a leckében szereplő terminológiára Gauss módszer), A - kiterjesztett rendszermátrix(azaz változók együtthatós mátrixa + szabad tagok oszlopa).
